CCF20090421006 (2)

		Iloczyn operacji symetrii jesi wy nikiem składania lub łączenia przekształceń symetrycznych, które polega na wykonaniu kolejno po sobie rozważanych operacji symetrii na tym samym obiekcie. iuiL{b|AHin TjyY?
ILOCZYNY OPERACJI
SYMETRII		^VXv_i^Tj
4. A. Rybr>ci}t-Pizrł |		Iloczyn dwóch operacji symetrii zawsze można zastąpić trzecią pojedynczą operacją symetrii. T,{UHU-} t2{u}={U") t3{u) = {U' ) . ^t2[t,{d}]=1U'5 = t3<u) T,®Tj = Tj 4 A. Rv4ijcr.t-Fvti 2

Przypomnienie - Kierunki elementów symetrii

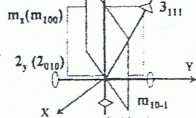
W symbolice kry stalograficznej kierunki elementów symetrii podaje się w indeksie dolnym np. 2, (2c.m)⁴z(⁴om) ³tti    »»i

y, z oznaczają kierunki dodatnich pótosi układu (osie układu mają wskaźniki: X [tOOj, Y [010]; Z [001 ]), natomiast cyfry np. 111, 101 to krystalograficzne wskaźniki kierunków (wskaźniki serii skierowanych prostych sieciowych)    _z

Dla płaszczyzny symetrii wskazany jest kierunek prostopadły do płaszczyzny

Dla osi obrotu wskazany jest kierunek równoległy do osi

(kierunek osi)

■'iwuur    J

dwukrotne wykonanie odbicia w płaszczyźnie lub obrotu o kąt 180’ można zastąpić tożsamością

PU Sh			j. Jfl*
,			X/ -*Y

x

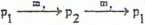
m_}. ® m_y = 1

1. A.    s

Przykłady iloczynów operacji symetrii

iloczyn obrotu i inwersji daje obrót inwersyjny n = n ® 1 3_Z g 1 = 3_Z 4_Z ® i = 4_Z 6_Z 8 1 = 6_Z ale 2_z®i = m_z(=2_z)

dwukrotne wykonanie inwersji można zastąpić tożsamością

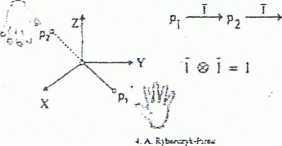
natomiast dwukrotne wykonanie obrotu o kąt 90° można zastąpić obrotem o kąt 180°

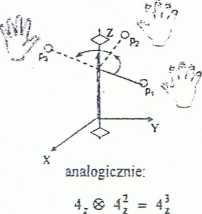
4,® 4,

3,® 3,

3;

6, = ói = 3,

4’ = 4? = 1    6_Z® 6_Z = 6_Z = 2_Z