CCF20091126031

drinż. Maria WŁODARCZYK

5

Ścinanie według PN-B-03264:2002

Wersjii 2004

Sporządzając obwiednie nośności prętów zbrojenia podłużnego można przyjąć, że siła w nich przyrasta liniowo na długości zakotwienia l_M.

drinż. Maria WŁODARCZYK

5

Ścinanie według PN-B-03264:2002

Wersjii 2004

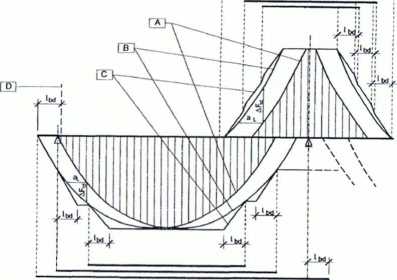
Rys. 4. Kształtowanie zbrojenia podłużnego w elementach zginanych z uwzględnieniem wpływu ścinania Siła rozciągająca w zbrojeniu bez uwzględniania wpływu siły poprzecznej Siła rozciągająca w zbrojeniu z uwzględnieniem wpływu siły poprzecznej Obwiednia nośności prętów zbrojenia podłużnego Krawędź podpory

A

B

C

D

2.6. Stopień zbrojenia na ścinanie p_x„ oblicza się ze wzoru.

P* = A-/ + Pw2 =

.v, b_w s₂ b_w sin a

(27)

w którym: A_sw, pole przekroju strzemion prostopadłych do osi elementu, leżących w jednej płaszczyźnie,

A_SW2~ pole przekroju strzemion ukośnych lub prętów odgiętych leżących w jednej płaszczyźnie,

s, - rozstaw strzemion prostopadłych do osi elementu,

s_:- średni rozstaw strzemion ukośnych lub prętów odgiętych mierzony wzdłuż osi podłużnej, a - kąt nachylenia do poziomu prętów odgiętych lub strzemion ukośnych.

Stopień zbrojenia na ścinanie nie może być mniejszy od wartości minimalnej wyznaczanej: na odcinkach drugiego rodzaju zgodnie ze wzorem (28)

(28)

na odcinkach pierwszego rodzaju zgodnie z ogólnymi warunkami konstrukcyjnymi.

2.7, Stan graniczny szerokości rozwarcia rys ukośnych będzie zachowany gdy spełniony zostanie warunek:

Ksw< K

d    E,f_A

(29)

gdzie: V_w,_im - graniczna siła poprzeczna powodująca ukośne zarysowanie o granicznym rozwarciu rys w u,,, = (0,1 -f 0,3) mm, p_wh p_w2 - stopnie zbrojenia poprzecznego,

E_s - moduł sprężystości stali: E, = 200 GPa, f ._k - wytrzymałość charakterystyczna betonu na ściskanie,

<J>i - średnica strzemion pionowych,

<j>₂ średnica prętów odgiętych i strzemion ukośnych,

iji, tj₂ współczynniki zależne od strzemion pionowych (f]i) i prętów odgiętych lub strzemion ukośnych (tj₂) równe:

1,0 - dla prętów gładkich,

0,7 - dla prętów żebrowych.

3. Ścinanie pomiędzy środnikiem a półką

W przekrojach teowych, gdy półka jest ściskana, oś obojętna przechodzi najczęściej niedaleko dolnej krawędzi tej płyty i naprężenia ścinające mają w półce dość dużą wartość. Ponieważ ścinanie wynika ze zmiany naprężeń (momentów), średnią siłę ścinającą na jednostkę długości oblicza się ze wzoru

	AF(l ^vsd = ~r~	(30)
	Ax
gdzie: AF,	r- zmiana siły podłużnej w półce po jednej stronie środnika na długości odcina Ax,
a)	gdy półka jest ściskana i xt./r< fyto:
	AFd =fcd xejfO,5(bu0— bw)	(31)
b)	gdy półka jest ściskana i xcff> hfto:
	SFd = fed hf0,5(beir- bw)	(32)
c)	gdy półka jest rozciągana to:
	SFd ^=fytl A ,	(33)

w którym: A, - pole powierzchni zbrojenia znajdującego się w półce po jednej stronie środnika. Aa - długość rozpatrywanego odcinaka

Długość odcinka Ax przyjmuje się nie większą niż:

połowa odległości między przekrojami M= 0 oraz M= | M_max I odległość między siłami skupionymi.

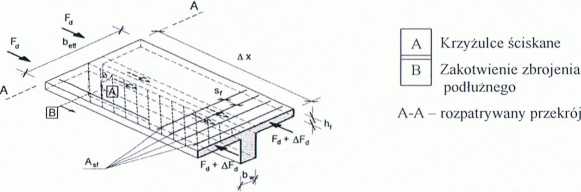
Rys. 5. Oznaczenia dotyczące połączenia półki ze środnikiem.

Siła ta jest przenoszona w przyjętym modelu przez ściskane krzyżulce betonowe i rozciągane cięgna stalowe. W belkach teowych role tych cięgien spełniają zwykle strzemiona znajdujące się w półce, a w stropach płytowo-belkowych - zbrojenie płyty nad belką.

Nośność krzyżulców betonowych sprawdza się z warunku:

v.sv/ ^ v_M2 =

YfcJ^h,

cotO

1 + cof² 0

(34)