CCF20091126037

Ścinanie według PN-B-03264:2002

Wersja 2004

dr inż. Maria WŁODARCZYK

3

1.4. Jeżeli element jest poddany ściskaniu, w tym również od sprężenia, to wartość Vm2 należy zredukować zgodnie ze wzorem (12) stosownie do obliczeniowej wartości V_R(,₂\

(12)

VRd2.red ~ CC_c VRd2

w którym:

./ cJ

a₍ = 1,25 a=2,5(\-^~)

fJ

dla 0 < <r_cp < 0,25 f_c,i dla 0,25 f_ctl < a_cp < 0,5 f_cl, dla 0,5 f_c,i < <j_ci, < 1,0/.,/ gdzie: cr_cl, - należy wyznaczać zgodnie ze wzorem (8) lub (9).

2. Elementy wymagające zbrojenia na ścinanie

Zbrojenie na ścinanie jest wymagane na odcinkach drugiego rodzaju.

2.1.    Jeżeli na jakimś odcinku elementu żelbetowego nie są spełnione warunki stanów granicznych nośności (1) i (2), to należy zastosować na tym odcinku, wymagane obliczeniowo, zbrojenie poprzeczne (strzemiona, pręty odgięte lub strzemiona ukośne). W belkach strzemiona ukośne lub pręty odgięte mogą być uwzględnione jako zbrojenie na ścinanie tylko wtedy, gdy strzemiona pionowe przenoszą co najmniej 50% siły Ksa-

2.2.    Stan graniczny nośności przekrojów elementów ścinanych, wymagających obliczeniowo zbrojenia na ścinanie, sprawdza się z następujących warunków:

Ksw <Vn,<2    (13)

Ksd<    (14)

gdzie: V_Rl(₃ - nośność obliczeniowa na ścinanie ze względu na rozciąganie poprzecznego zbrojenia na ścinanie.

W przypadku wystąpienia siły podłużnej nośność należy sprawdzać z warunków:

Vnd2.red    (15)

Vsd^yRd3    (16)

2.3. Obliczeniowe nośności przekroju na ścinanie z uwagi na zmiażdżenie ściskanych krzyżulców betonowych V_M3 i z uwagi na zbrojenie poprzeczne V_MJ określa się ze wzorów:

- jeżeli zbrojenie na ścinanie składa się wyłącznie ze strzemion prostopadłych do osi belki (tzn. gdy nie stosuje się prętów odgiętych lub strzemion ukośnych, lub pomija się wpływ tych prętów):

i/ r l CO/0 VrJ! = vf„, b„ z --— 1 + col 0	(17)
yUd3 yRd3l Z COtO	(18)

jeżeli zbrojenie na ścinanie składa się wyłącznic ze strzemion ukośnych to nośności V_litl2 i V_R<i₃ oblicza się ze wzorów.

Vr,!2 = vf_cdb_wZ

(19)

(20)

cod) + cola I + col²f)

A f

V,_W3--^tW-z {cotO + cola) sina

jeżeli zbrojenie na ścinanie składa się ze strzemion prostopadłych do osi belki oraz z prętów odgiętych lub strzemion ukośnych:

>V’ = vfc.tb„z

cotO

w którym

1 + co! O

VIW ~ V,«m ⁺ yK<I32

+ AV

: cos a < vf,i b_w z

cotO cota

(\ + corO) (2cotO A- cota)

(21)

(22)

(23)

W przypadku działania ściskającej siły podłużnej Ns,i wartość V_M3 ze wzorów (19) i (21) należy zredukować do Vn,i2,_mt zgodnie ze wzorem (9).

Oznaczenia we wzorach od (17) do (23):

v - współczynnik określony według wzoru (11),

a    - kąt nachylenia prętów odgiętych lub ukośnych strzemion,

A_swi    - pole przekroju poprzecznego prętów tworzącycli jedno strzemię prostopadłe do osi elementu

(np.: pole czterech prętów <j) 6 w przypadku strzemion podwójnych <|> 6), fywdi - obliczeniowa granica plastyczności strzemion prostopadłych do osi elementu, s, - rozstaw strzemion prostopadłych do osi elementu,

A_Sw2 - pole przekroju poprzecznego ukośnych strzemion lub prętów odgiętych tworzących jedną płaszczyznę odgięć,

3j - średni rozstaw płaszczyzn odgięć lub strzemion ukośnych mierzony wzdłuż osi belki, fyrij - obliczeniowa granica plastyczności zbrojenia A_sw2.

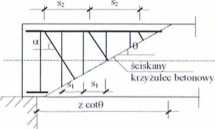
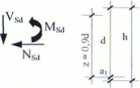
Rys. 3. Podstawowe oznaczenia wykorzystane we wzorach od (17) do (23)

2.4.    Kąt a zbrojenia poprzecznego uwzględnianego w obliczeniach nie może być mniejszy niż 45°, kąt 0 można dobierać dowolnie z przedziału określonego nierównością:

1,0 < cot0 <2,0    (24)

2.5.    Zbrojenie podłużne w każdym przekroju poprzecznym elementu powinno być zdolne do przeniesienia sumarycznej siły rozciągającej F_lt/ obliczonej z uwzględnieniem siły poprzecznej AF„i-Wpływ siły poprzecznej na wzrost siły rozciągającej w zbrojeniu podłużnym określa się według wzoru:

AF„, = 0,5Kh \cot0 - ^2-co/a    (25)

V    )

Na długości elementu, gdzie moment zginający nie zmienia znaku, sumaryczna siła rozciągająca w zbrojeniu podłużnym F_ul nie może przybierać większej wartości niż wartość bezwzględna maksymalnej siły rozciągającej wywołanej działaniem momentu zginającego i siły podłużnej.

W elementach ze zbrojeniem na ścinanie wpływ siły poprzecznej oblicza się ze wzoru (25), lub poprzez poszerzenie wykres sił o odcinek a_L przyjmując:

a, = 0.5 z cotO - ^1-cota    (26)

l ^v*n )

W elementach bez zbrojenia na ścinanie wpływ siły poprzecznej można uwzględniać poszerzając wykres sił o odcinek a_L = d