CCF20110307005

=?)

Ma i iłu i 'iłujący dominantę ma żalem postać:

l) = x_D +

gi> -gi

- ■ Ax,

8n Sd-i ⁺8d g d+i

Dla następującego szeregu statystycznego wyznaczyć dominantę metodą analilyi. uą i graficzną.

Xi	20-30	30-50	50-80	80-100
ni	10	40	45	20

o......i' l ina .ą analogiczne jak w zadaniu 6.

IJt lliiM i iii pi /.V|wtclkii otrzymaliśmy:

Źródło: dane umowne Rozwiązanie

Przedstawiony szereg statystyczny nie spełnia założeń niezbędnych do wyziuiczculii dominanty w oparciu o wzór przedstawiony w zadaniu 6, gdyż przedziały klasowe nic 'u| równej długości. Konieczne jest zatem przeprowadzenie pewnego rodzaju proecdill normalizujących przedstawiony szereg, czyli odniesienie liczebności cząstkowych do jednostki długości przedziału klasowego, co oznacza zastąpienie liczebności tzw. gęstoścliiliil przedziałów (oznaczającymi dokładnie natężenie liczebności na jednostkę długości przedziału klasowego). Gęstości oznaczamy symbolem gj i wyznaczamy jako ilorazy liczebności i długości poszczególnych przedziałów.

gi =

AX;

i = 1,2.....k

2-1    1,0

I) 30-1---20 = 30 + —-20 = 43,33

2-1+ 2-1,5    1,5

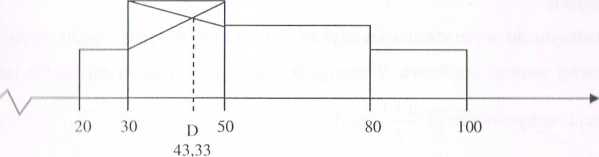
■Wuli w moloil/.ic graficznej otrzymamy odpowiednio:

Mamy zatem odpowiednio:

Axi = 10    Ax₂ = 20

10

⁸'⁼7T

40

20

Ax₃ = 30

⁴⁵    , s

g₃ =— = 1,5

³    30

Ax₄ = 20 20

g₄ =

20

Warto przy tym zauważyć, że nastąpiło przesunięcie dominanty: z trzeciego przedziału u granicach 50-80 do drugiego o granicach 30-50 (przedział dominanty to przedział o największym natężeniu liczebności cechy na jednostkę długości przedziału klasowego co w przypadku przedziałów o równych długościach pokrywa się z największą liczebnością cząstkową).