CCF20130109045

oraz

^Wmax — ^Udop >

gdzie:

^max * ^dap

(6.15)

maksymalne przemieszczenie osiowe przekroju pręta oraz jego wartość dopuszczalna.

PRZYKŁAD 1

Sporządzić wykres sił normalnych w pręcie obciążonym jak na rysunku 6.4, jeżeli P\ = 60 kN, P₂ = 40 kN, l = 0,5 m. Zaprojektować wymiar a przekroju pręta i obliczyć całkowite wydłużenie pręta. Narysować rozkłady naprężeń w przekrojach a - a i P - p .

Dane: k_r = 100 MPa, £ = 2 • 10⁵ MPa.

a)

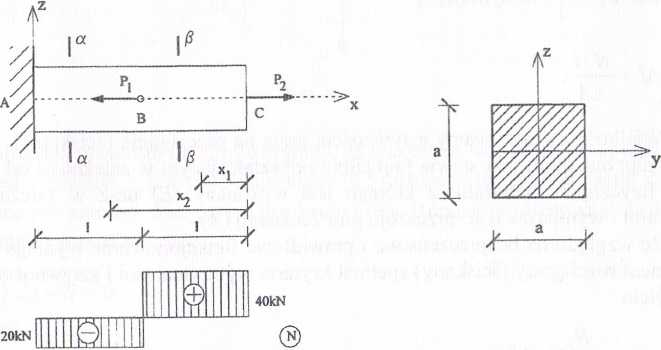
Rys. 6.4

W rozpatrywanym pręcie wyróżniamy dwa przedziały: CB i BA. W każdym przedziale prowadzimy myślowy przekrój, a następnie zapisujemy funkcję N(x) w tych przekrojach. Mamy:

dla x, e < 0, /) JV(xi) = P₂ - 40 kN,

dla x₂ e < 1,21 > , N(x₂) =P₂~P\ = -20 kN.

Wykres N(x) pokazano na rysunku 6.4b.

Warunek bezpieczeństwa dla pręta rozciąganego ma postać

^max

N_n

A

■<k_r.

yV,_nax odczytujemy z wykresu sił normalnych. W rozpatrywanym przykładzie N_maK = 40 kN. Naprężenia dopuszczalne dla materiału, z którego wykonano pręt wynosz;

100. MPa = 10

kN

, zatem

cm

40

<10,

stąd

a>.

a > 2 cm .

Przyjmujemy jako wymiar przekroju a = 2 cm.

Całkowite wydłużenie pręta obliczamy jako sumę zmiany długości poszczegól nych odcinków pręta

Al = Al_AB + Al_BC,

przy czym

A_U=^₌(M ₌ -0,0,25cm,

AB _RA    ---a .

2-10 -4 _    ■ l_BC _ 40•50

= 0,025 cm.

EA    2-10'^ł -4

Ostatecznie

Al = -0,0125 + 0,025 = 0,0125 cm.

Naprężenia w zadanych przekrojach pręta wynoszą odpowiednio:

a-a 20 kN cnn/m o_x =--= -5—r- = -50MPa,

4    cm

<r_x^p~^p = — = 1 0^L = 100 MPa. 4 cm²

8'