CCF20130109070

Warunki równowagi

Wytnijmy dwoma myślowymi przekrojami normalnymi do osi pręta, element o długości dx. Na lewym końcu elementu działa moment skręcający M_x, na prawym elementarne siły wewnętrzne T_pdA - rysunek 6.59.

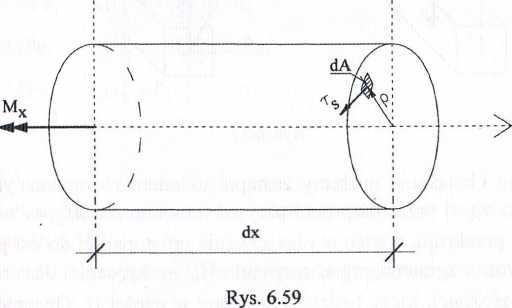
Warunek równowagi rozważanej części pręta ma postać

jfppdA-M_x = 0.    (6.37)

W

Warunek geometryczny

Odkształcenie pręta skręcanego polega na obrocie poszczególnych jego przekrojów względem siebie. Kąt wzajemnego obrotu przekrojów końcowych nazywamy kątem skręcenia <p pręta.

Rozpatrzmy odkształcenie pierścienia o szerokości dx, promieniu p i grubości dp (rys. 6.60).

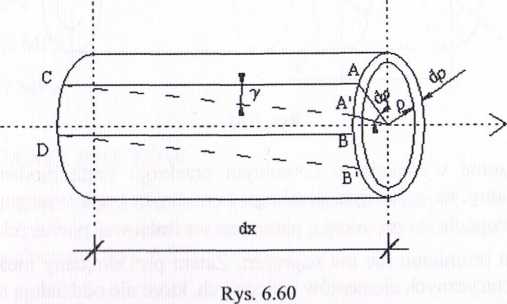
wyoaręnmjmy na jego powierzcnni prostoKąt Atsou, Kiory po odkształceni u stanie się równoległobokiem A’B’CD. Długość łuku AA’ jest równa y • dx oraz p ■ dę. Wynika stąd warunek geometryczny

y ■ dx = p ■ d(p .    (6.38)

Związek fizyczny

Zgodnie z prawem Hooke’a mamy

T, =G-y,    (6.39)

gdzie:

G - moduł sprężystości poprzecznej zwany modułem Kirchhoffa.

Z zależności (6.38) wyznaczamy y i podstawiamy do wzoru (6.39), co daje

_ dę

^=GP~~r-    (6-40)

ax

Podstawiając powyższy związek do równania równowagi (6.37) i uwzględniając,

że G^~- nie podlega całkowaniu, a [ p¹dA = I₀ , otrzymujemy kolejno:

*    M

G^\p'-dA-M_r=<>,

(A)

G^1₀=M_X,    (6.41)

dę ₌ M_x

dx G-1₀

Iloczyn G ■ I₀ nazywamy sztywnością pręta na skręcanie.

Podstawienie (6.41) do (6.40) pozwala uzyskać zależność opisującą rozkład naprężeń stycznych w przekroju kołowym pręta, poddanego skręcaniu

=

M_x-P

Io

(6.42)

Naprężenia styczne T_s są liniową funkcją promienia p i osiągają maksymalną wartość w punktach najbardziej oddalonych od środka ciężkości przekroju, to jest

137