df3

Rozdział 4

Zadanie 3

Wyznaczyć pochodną funkcji:

a) f(x) = x³ + 2x² - 1 f(x) = 3x² + 4.r

b)/(x) = x + i

/(*) = 1-4-

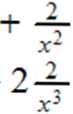
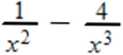
c)/(.r) = x⁵-n⁵ f(x) = 5x⁴

d)/(x) = 41nx-2/gx

/W = f -

COS~Y

^e)A^x) = arctbgx - 2 smx

/W = —4 - 2cosx 1

f) /(x) = xc/gx f (x) = c/gx +

srn^Y

g) /(x)= X² • e*

/(X) = 2xe^x + x²e^x

h) /(x) = (*² + *)(3 cosx + 2)

f(x) = (2x + 1)(3 cosx + 2) - 3 sinx(x² + x) = = 6xcosx + 4x + 3 cosx +2 - 3x² sinx - 3xsinx

i)/(x) = xjx • (x² + 2)

f(x) = [Jx + (x • -^r-)](x² + 2) +xjx • 2x =

= [x²7I + 2^ +    + 7^] + 2x²yF = 7I(fx² + 3)

j )A^X) = Jxlnx-xarcsinx

f{x) = ^ + nr - (arcsinx +

= -^rr + Ąr - arcsinx ———

jx    yr?

k) Ar) = ^

/?(_r\ ₌ 2y(y-1)-(y²+1) ^J ^ '    (y-1)²

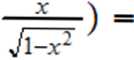
■Y--2.Y-1

!)/(*) =

_    Y~~Y²~h 1

Y--Y

—    C³*²"²* ) (y²-y)-(y³-y²+ 1 )(2y- 1)

(y²-y)²

_    3y~-3y--2y ³+2y ² -2y⁴+y ³+2y ³-y²-2y+1

(y²-y)²

3Y⁴-3Y^:>-2Y³d-2Y²-(2Y⁴-Y³-2Y³-hY²+2Y-l)

(y²-y)²

y⁴-2y-4y^:-2y+1

y²(y-1)²

_ sinY+1

Y

m)/(x) =

_ (cos y)y-(suiy+ 1)

YCOSY-sillY-l

Y^x

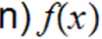
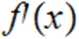
Jy+2 arctgx

(2^r)^gx-( Jx+2)( -^y) arctg~x

_1___-/r+²

2 Jy arcfg*    (1 +y² )arctg²x

(Jy+2)(-L-) arctg²x    arctg²x

°)M - ^ +

/(.v) -    +

Y

Y+l

Y+1)~Y

(Y+l)²

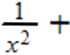
1

(Y+l)²

_    2y^:+2y+1

y²(y+1)²

(y+1)²+y²

y²(y+1)²

P)/W = 4F

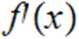
_ g^y(CQSY-YsinY)-g^X(YCOSY) _ g*(cos y-y sinY-Y cos y) g²*    e²*

_ COS Y-Y sillY-Y COS Y q)/(x) = (2x+ l)⁷

/(x) = 7(2x + l)⁶ -2 = 14 • (2x+ l)⁶

15x⁴ =

15.v⁴

cos²(3y-)

0 A*) = tg(3x⁵) f(x) =    *    •

cos^(3y^)

S)Ax) = V+r² + 3

/W = 4— •^8x = -7=

2j4x^+3    J4x^z+3

t)/(x) = e*^{2 1} /(x) = e*²"¹ • 2x

u)/(x) = ln(2x² + 1) f(x) =

l

2y²+1

4x =

4x

2y²+1

v)f(x) = sine^3x

f(x) = cose^JY • e^JY • 3 = 3ć^3y • cos£^3y