DSC07058 (4)

52

Ciągi liczbowe

sj m    •. h) lim fS-M) ^ł’ⁿ;

•-*1 +3+ ... + <2n - 1)    ^/»—« V " /

i    i

T&»-1)

i) Hm (1 +2* —3*).    j) lim > .”—:-r;

■—    ⁷    »—oc n [fai(n + I) — In nj

039i-    /gji ł A ⁿ*^ł    I

k) lim    *;    |) lim (-J ; m) lim sin" —.

•    «\ n /    «—o® n

2>tefeU3

Zoakfć zbiory punktów skupienia (właściwych i niewłaściwych) podanych ciągów:

Łi21ⁿ

Brl

»)«*=*

. < nr

b) 6n = sur —;

c) c^= U + C-lrJ-2^; d)d_n = (ł-r ^f^^:)^S:

«)    * (-ir:    o ifa = cos^;

g)z««2*-i-(-2)\    h*) kw = JZ-E(i/ń);

_-lit 1-14

Znałeś |nci<T dolce i górne podanych ciągów;

»ł«.-f-ir(»* + i); b)ł. = n^-²ⁿ^'—;

c}e. = ^{^'i ^:    «9 <i. = (l+co«rer)n!;

«}*. =    O ft. = [ł+(-»r] «:

g)    » wa jjjSpj    h) vn **(~5)^m + l :

f») w_: = 0.1. w} *0 22, trj = 0.333,..u^t «= 0j5X5^.. ló.... ;

pitUłfcl* J5*

J*) Im “ pierwa&a cyfra w zapiaie dziesiętnym liczby n.

Granice funkcji

Przykłady

Definicje ciągowe granic funkcji

• Przykład 2.1

Korzystając z definicji Heinego granicy właściwej funkcji uzasadnić podane równości:

a) lim (2x — 7) = 1; b) lim = 2; c) lim sin z = 0;    d*) lim e* = e*.

Rozwiązane

W Rozwiązaniu wykorzystamy definicję Hdnego granicy włafciwej /unkcjl /;

«* -4 4=4    =*    =«*

śdzle a jest jednym z symboli    "°°* oo, zaś 4 ^c

•) Mamy pokazać, i*

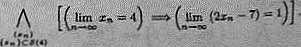
53