DSCN0767

przedłużymy te krawędzie, to zauważymy, że zbiegają się one w każdej gj^ pie w jednym punkcie: poprzeczne i podłużne krawędzie zbiegają się w pu_n, ktach Zj i Z_s, a pionowe w punkcie Z₃ (poza płaszczyzną rysunku).

Punkty Z₂, i Z₈ nazywamy punktami zbiegu: punkty Z_x i Z₂ znajdują się na jednej prostej h poziomej, stanowiącej krawędź przecięcia się płaszczyzny horyzontu z płaszczyzną tłową.

3.3. RZUTOWANIE AKSONOMETRYCZNE 3.3.1. Rodzaje rzutów aksonometrycznych

Metoda rzutów prostokątnych umożliwia nam odwzorowanie przedmiotu na płaszczyźnie rysunku najczęściej w rzutach na trzy płaszczyzny wzajemnie do siebie prostopadłe w ten sposób, że większość krawędzi przedmiotu rzutuje eię bez skrótów lub skraca się całkowicie (do zera). Rysunek taki nie może odwzorować bryły w jednym rzucie, gdyż rzut przedstawia tylko jedną stronę przedmiotu, nie nadaje się więc do jej poglądowego odwzorowania.

Rzuty aksonometryczne (słowo aksonometryczny pochodzi z greckiego akson — oś i metreo — mierzę) natomiast odwzorowują kształt przedmiotu w jednym rzucie, przedstawiając jego trzy podstawowe wymiary (wysokość, szerokość i głębokość) w jednej płaszczyźnie zwanej rzutnią aksonometryczną.

Rzutnia aksonometryczna n_a jest płaszczyzną dowolnie ^ustawioną względem trzech głównych płaszczyzn rzutowych tc₂, m układu prostokątnego

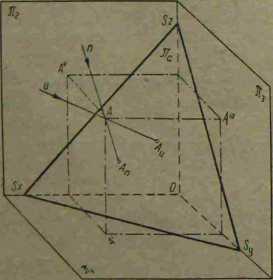
Rys. 3-5. Płaszczyzna rzutów aksonometrycznych

(rys. 3—5). Ślady h, r, k płaszczyzny 7i_a utworzą na tych rzutniach trójkąt zwany trójkątem śladów.

Przyjmijmy dowolny .punkt A W przestrzeni odwzorowany przez jego rzuty prostokątne A', A" i A"' (rys. 3—5). Na rzutnię aksonometryczną n_a możemy wykonać nowy rzut punktu A w kierunku n prostopadłym do niej-łub w kierunku u ukośnym. W pierwszym przypadku mówimy o aksonometrii prostokątnej, a w drugim o aksonometrii ukośnej. Rzut A_n nazywamy rzutem aksonometry c/nym prostokątnym punktu A, a rzut A_u — rzutem aksonome-trycznym ukośnym punktu A.

Rzut aksonometryczny jest zawsze ściśle związany z rzutami aksonometrycz-nymi trzech osi układu prostokątnego. Przystępując do wykonania rysunku ak sono metrycznego, musimy najpierw narysować rzuty aksonometryczne X YZ trzech osi układu prostokątnego xyz. Pomijając wyliczane teoretycznie skrócenia aksonometryczne, omówimy praktyczne wskazówki dotyczące n a stępujących rodzajów rzutów aksonometrycznych, stosowanych w rysunku technicznym maszynowym: a) rzut ukośny, b) rzut prostokątny jednomiaroicy, c) rzut prostokątny dwumiarowy,

3.3.2. Rzut ukośny

Wśród rzutów aksonometrycznych ukośnych najbardziej rozpowszechniony jest rzut ukośny zwany również perspektywą równoległą. Na rys. 3—60 przedstawiono układ osi współrzędnych XYZ. Dla odwzorowania przedmiotu będziemy rysowali równoległe do osi Z te krawędzie przedmiotu, które w rzeczywistości są pionowe, a równoległe do osi X i Y krawędzie poziome wzajemnie

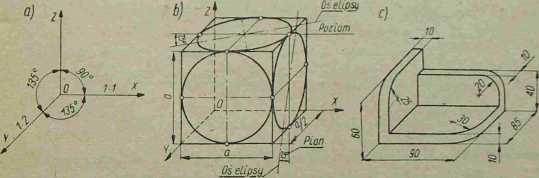
Rys. 3-6. Sześcian w perspektywie równęleglej (rzut ukośny)

prostopadłe; przy czym krawędzie równoległe do osi X i Z przedstawiamy na rysunku bez skróceń (1 :1),' a krawędzie równoległe do osi Y" w dwukrotnym skróceniu (1 :2).

Według tych założeń przedstawiono na rys. 3—66 obraz sześcianu z wpisanymi w jego ściany okręgami kół.

w przybliżeniu 1 : 3 o osiach niekiedy

Rzuty kół leżących w płaszczyznych równoległych do płaszczyzn XOY i YOZ stają się elipsami o stosunku osi nachylonych do osi pionowej Z lub poziomej X pod kątem «ś 7\

Rysunek 3—6c przedstawia przykład przedmiotu odwzorowanego w rzucie ukośnym.

3.3.3. Rysowanie figur płaskich w rzucie ukośnym

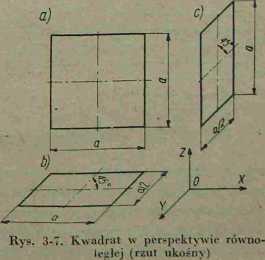
Rys. 3—7 przedstawia kwadrat w rzucie ukośnym, zajmujący trzy położenia równoległe do płaszczyzn określonych osiami XYZ. Kwadrat zajmujący położenie równoległe do płaszczyzny

4* 51