DSCN1137 (3)

2) Niech daną prostą spełniającą warunki zadania będzie prosta EG.

Ponieważ prosta CD zawiera środkową, zatem *s.adc — P^bdc.

Wobec tego prosta EG będzie dzieliła pole A ABC na połowy wtedy, gdy

PV£DO ⁼ P^CGO,

a także będzie, gdy |£G| = |GC| (uzasadnienie pozostawiamy Czytelnikowi).

Ponieważ

;) + P*

P^FBG — VtkDBC Pk EDO ⁼ PS.OGC,

więc

*SEBG ⁼ *b.DBC,

zatem

i|£B|-|GB|-sin45⁰ =i|DB||DC|.

Przyjmując oznaczenia \DB\ = \DC\ # a,

\ED\ = \CG\ =

powyższa równość przyjmuje postać

Ca + x)(a_y/2-x)Y = a².

skąd po przekształceniu otrzymujemy: x = 0 lub x = a(y/2 — 1).

Rozwiązanie x = 0 daje prostą CD, o której mowa w 1). Ponieważ AADG = ABDG, zatem oprócz prostej EG (przy spełnieniu warunku x = a(J2 — 1) istnieje prosta FH symetryczna do EG względem prostej CD. Zauważmy, że rozwiązaniem są proste prostopadłe do boków trójkąta.

CMp. 3 proste: j^j = y/2 — 1, £§ = >/2+l,

5.23. Niech \AB\ = c. |BC| = a, \AC\ = b (rys. 5.23). Wtedy to

\AD\

\DE\

\ABC

2 2

tkAOC

ar.

E.BOC * SAOB

^r = ^(b + a-_c)>

gdzie r_c oznacza

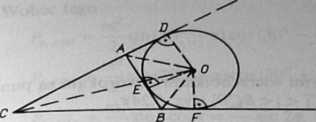
Rys. 5.23

długość promienia okręgu stycznego do boku o długości c.

Ze wzoru Herona_'/

P^abc = y/p(P — «)(P - ^b)iP — ^c)>

a + 6 + c gdzie p =-^-

.    , . b + a — c

oraz równości---= p — c

otrzymujemy P k a nr

p — c Podobnie

p(p - o)(p — c) P c

r_b = j ^ra = j

pip — a)(p — c)

p(p-fe)(p-c)

P - «

Oznaczając przez r długość okręgu wpisanego w trójkąt, mamy: ______ _S

P

P~a

S

p-b

S

P-c

, a stąd

r S

1 p — a

1 __ p — b

r_b^_ S

1 p — c

zatem

J. 1 3p — a — b — c 3p — 2p p

^r« r_h* 7 ~ S ⁼ Ś ⁼ S

131