DSCN1617

-vv

li-rt

132

7. Zasady obliczeń wytrzymałoś* iowych śrub

71 Obliczenia śrub rozciąganych i skręcanych

133

W przypadku połączenia śruby dwustronnej z nagwintowanym gniazdem korpusu można przyjąć Dfnoo. Wówczas powyższy wzór przyjmie postać

_ w__1_

^Pfl * iza ₊ i±a '    (7.17)

E, Et

Gdy materiai śruby i korpusu jest taki sam (E_l = E₂ = E, y, = r*) wzór (7.17) ma postać

S--    <⁷-¹⁸>

Moment skręcający 3f, jaki trzeba przyłożyć, aby dokonać połączenia, wynika z sił tarcia na bocznych powierzchniach gwintu. Nacisk p. na tych powierzchniach (rys. 7.12) jest równy

^Po==?°~ŹT'    t^U9)

gdzie P — jest podzialką gwintu, aa — rzutem boku gwintu na oś.

W gwincie metrycznym P/2a = 8/5, gdzie p, = Bp Jo. Powierzchnia

tarcia jednego zwoju gwintu wynosi F = 2 ~ (d*—d/)/cos £ ; (oznaczenia podano na rys. 7.12).

Warunek wytrzymałości dla śrub poddanych działania sil osiowych Q z jednoczesnym skręcaniem momentem M wedhłg hipotezy Hubera określa nierówność

OEl)

Q

gdzie oj jest naprężeniem zastępczym, o=-naprężeniem rozciąga-

7*

jącym lub gdakającym, r — naprężeniem skręcającym, a k, i K, są dopuszczalnymi naprężeniami przy skręcaniu oraz przy razdąganiu k, hib ściskaniu fc_Cf dj jest średnicą wewnętrzną gwintu śruby.

Zasady określania dopuszczalnych naprężeń podano w punkcie 72.

Ł

Przy obciążeniu statycznym t— —1,7 (hipoteza Hubera) wzór (721) ma postać

o. = )W3i*<lc^    (722)

Naprężenia skręcające w zakresie odkształceń sprężystych (ryt. 7.13ai wyznacza się ze wzoru

M

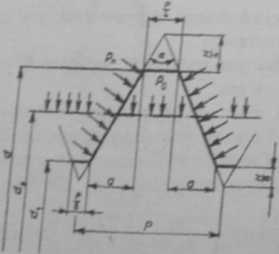
Ryz. 7.12. Nacisk na bocznych powierzchniach gwintu pasowanego ciasno

(7.20)

(rys. 7.13c), naprężenia skręcające są równe

M

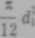
O)    b)

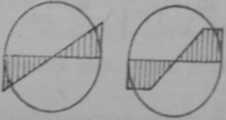
^H>^s- 7.11 Rozkład naprężeń skręcających w śrubie: a) w zakresie odkształceń sprężystych, b) w zakresie odkształceń sprężysto- plastycznych, c) w zakresie odkształceń plastycznych

8da tarcia przy n zwojach gwintu na długości skręcenia i współczyn niku tama p jest równa T—f/p_nF_nt a stąd moment tarcia

M=r-

COS —

2

Jeśli w całym przekroju rdzenia śruby zachodzą odkształcenia plastyczne

(724)

0

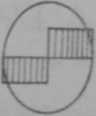
W tym przypadku zachodzi równość

r'o»+3«»*R_w    (725)

gdzie R, jest granicą plastyczności