DSCF6553

62

Gaussa o parametrach n_k = \ i = «*.*> gdzie 1= 1,2. Rozpatrzmy różnicę średnich jtj i x₂:

z = x,-xj    (4j

Wartość oczekiwana i dyspersja funkcji liniowej    n niezależnych zmiennych

losowych wyrażają się wzorami (por. np. [7]):

E[Za,xJ = Za^IjcJ = lii    (5)

= ZafP[xJ    (6)

Z ostatniego związku wynika w szczególności wzór 3.

Dla prostej kombinacji liniowej dwu zmiennych losowych x_L i 5, otrzymamy:

E[z] =^-*2    I

o\ = ol+el    I

1 2

Sprawdźmy, czego można oczekiwać w wypadku, gdyby obie populacje monet były jednakowe. Sformułujemy natępującą hipotezę: „wartości średnie mas monet w obu populacjach są jednakowe, a różnice stwierdzone w doświadczeniu, wynikają ze skończonych rozmiarów próbek”.

Jeśli nasza hipoteza jest prawdziwa, wartość oczekiwana zmiennej z wynosi zero: E[z] = 0. Wobec tego zmienna losowa u, określona następująco:

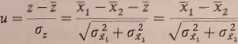
będzie podlegała rozkładowi normalnemu o zerowej wartości średniej i jednostkowej dyspersji.

2. Pomiary i opracowanie

Do pomiaru mas monet posłuży nam precyzyjna waga automatyczna. Wyniki otrzymane dla monet każdej grupy (liczebności obu grup powinny być zbliżone i wynosić 20-4-30 monet) należy przedstawić w formie histogramu. Szerokość przedziału histogramu wybieramy tak, aby kwadrat liczby klas był bliski liczbie pomiarów. Po obliczeniu wartości parametrów (wzory 1 i 2) rysujemy na tle histogramów rozkłady normalne.

Dla znalezionej z wzoru 9 doświadczalnej wartości u₀ zmiennej u odczytujemy w tabl. 11 prawdopodobieństwo tego, że u>u₀¹. Jest to prawdopodobieństwo pojawienia się zaobserwowanej eksperymentalnie różnicy pomiędzy średnimi w wypadku, gdy nasza hipoteza o równości średnich wartości populacji jest prawdziwa. Zwykle przyjmuje się 0,05 jako wartość graniczną, tzn. w wypadku, gdy prawdopodobieństwo P(u>u₀) okaże się mniejsze od 0,05 hipotezę należy odrzucić.

Pytania

1.    Jak można zapisać wzory 1 i 2 dla przypadku, gdy znany jest tylko histogram wyników? Na czym polega niedokładność takich formuł?

2.    Czy wartość u₀ uległaby (prawdopodobnie) zwiększeniu, czy zmniejszeniu, gdyby pomiary wykonywano na wadze o mniejszej dokładności (większym rozrzucie)?

ST-3. Rozkład oporności oporników - eksperyment statystyczny [101

1. Wstęp

Pomiar oporności oporników fabrycznych o określonym nominale będzie dla nas pretekstem do wykonania prostego eksperymentu statystycznego. Będziemy badali oporniki węglowe, otrzymywane przez napylenie warstwy węgla na podłoże ceramiczne. Zgodnie z obowiązującymi normami, produkowane są oporniki o nominalnych wartościach oporności tworzących trzy w przybliżeniu logarytmiczne szeregi z tolerancją 20%, 10% i 5%. Ponieważ nominały oporników z ostatniego szeregu różnią się o ok. 10%, oznacza to, że każdy wyprodukowany egzemplarz można, po dokonaniu pomiaru oporności, zakwalifikować do określonej grupy: może to więc być produkcja całkowicie pozbawiona braków.

Rozpatrzmy próbkę np. 150 oporników, wybranych przypadkowo z dużej serii. Nieuniknione fluktuacje w procesie produkcji powodują, że zmierzone

1

Ponieważ interesuje nas obustronne ograniczenie, tzn. przypadek |u| > u₀, odczytaną w tabl. II wartość należy pomnożyć przez 2.