dupa0035

Na każdego pracownika zatrudnionego w 1992 r. w Wojsku Polskim przypadło średnic miesięczne wynagrodzenie w wysokości 3,98 min zl,

Średnia arytmetyczna charakteryzuje się różnymi własnościami, z których wymienimy najważniejsze.

• Jako wypadkowa wszystkich zaobserwowanych wartości cechy średnia arytmetyczna jest parametrem klasycznym i przyjmuje wartości z przedziału:

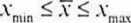
• Suma odchyleń wartości cechy od średniej arytmetycznej równa się zero:

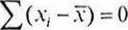
(2.17)

• Jeżeli wszystkie wartości cechy X pomnożymy przez dowolną stalą a (a ź 0), to średnia arytmetyczna nowej zmiennej Y będzie a razy większa od średniej arytmetycznej zmiennej X:

(2.18)

Na przykład średnią cenę jakiegoś towaru wyrażoną w złotych możemy, mnożąc przez odpowiedni przelicznik, wyrazić w dolarach.

• Jeżeli do wszystkich wartości cechy dodamy dowolną stalą b, to średnia arytmetyczna nowej zmiennej Z będzie różnić się od średniej arytmetycznej zmiennej Xo tę samą wartość:

(2.19)

Na przykład średnia temperatura wyrażona w skali Farenheita może być wyrażona w skali Celsjusza.

• Suma kwadratów odchyleń wartości cechy od jej średniej arytmetycznej jest mniejsza niż suma kwadratów odchyleń od jakiejkolwiek innej stałej:

(2.20)

Średnia harmoniczna

Średnia harmoniczna jest odwrotnością średniej arytmetycznej, obliczonej z odwrotności wartości cechy. Dla szeregu szczegółowego liczymy ją następująco:

n

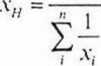
(2.21)

Natomiast dla szeregu rozdzielczego posługujemy się wzorem na średnią

ważoną:

n

(2.22)

Jest to miara klasyczna, obliczana na podstawie wszystkich obserwacji.

Średnia harmoniczna jest stosowana rzadko, bowiem może być ona zastąpiona średnią arytmetyczną ważoną odpowiednimi wagami, co zostanie pokazane na przykładzie obliczania średniej ceny jaj. Informacje o cenie można bowiem podawać na dwa sposoby, które są wzajemnie odwrotne, tzn. można podać, ile jednostek towaru można nabyć za odpowiednią kwotę, bądź też można podać cenę jednostki towaru. W pierwszym wypadku posłużymy się średnią harmoniczną, natomiast w drugim - średnią arytmetyczną. Należy zauważyć, że średnia harmoniczna dla pierwszego sposobu jest równa odwrotności średniej arytmetycznej, obliczonej z informacji podanych drugim sposobem.

1*2.7. Na podstawie obserwacji przeprowadzonej w trzech sklepach stwierdzono, że za 10 tys. zJ można w pierwszym nabyć 5 jaj (.V,), w drugim 4 (.\'₂). a w trzecim 6

65