dupa0050

——-—►

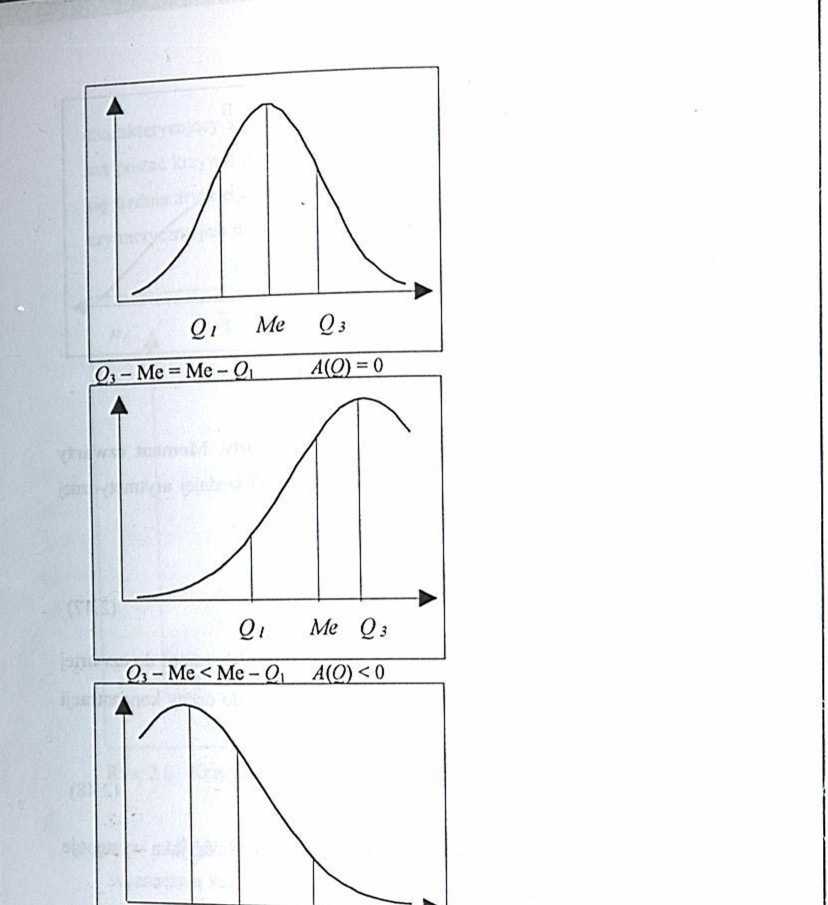
Q i Me    Q₃

^3 - Mc > Me - O) A(O)>0 Rys. 2.7. Położenie kwartyli w rozkładach o różnej asymetrii

Należy zwrócić uwagę, że omawiana miara asymetrii dotyczy tylko połowy badanej zbiorowości, czyli jednostek, które mają wartości cechy zawierające się między kwartylem pierwszym i kwartylcm trzecim.

W podobny sposób jest skonstruowana druga pozycyjna miara asymetrii, czyli współczynnik asymetrii wykorzystujący decyle:

₌ (D_q-Me)-(Me-D_]) ₌ (P, - Me) - (Me - D,) ^K ;    P,-P,    (D₉-Me) + (Me-D_t)

(2.46)

Współczynnik ten opiera się na założeniu, że w szeregu symetrycznym decyl pierwszy ( D\ ) jest tak samo oddalony od mediany ( Me ) jak decyl dziewiąty ( P₉ ). Uwzględnienie w obliczeniach rozstępu międzydccylowcgo sprawia, że omawiana miara pokazuje asymetrię środkowych 80% zbiorowości.

Oba współczynniki asymetrii zbudowane na podstawie kwantyli przyjmują wartości z przedziału (-l;+l).

P2.23. Wykorzystując obliczone w 1*2.15 kwantylc rozkładu wynagrodzeń za wrzesień 1992 r. pracowników zatrudnionych w polskiej gospodarce, zbadamy asymetrię rozkładu, w którym: Sie = 2773 tys. zł ; 0\ = 2129 tys. zł; Oj = 3696 tvs. zł; D\ = 1679 tys. zł: D₉ = 5091 tys zł.

A. Obliczamy współczynnik skośności oparty na kwartylach - wzór (2.45): _un. _ (3696 - 2773) - (2773 - 2129)

^    (3696-2102)

Środkowe 50% rozkładu plac, odnoszące się do pracowników, którzy zarabiali nic mniej niż 2129 tys zl (0\) i nie więcej niż 3696 tys zł (O3). charakteryzuje się niewielką dodatnią asymetrią.

13. Obliczamy współczynnik skośności oparty na decylach - wzór (2.46):

₌ (5091- 2773)-(2773-1679) ₌

^ ’    5091-1679

Poszerzenie zakresu analizy na środkowe 80% rozkładu, czyli na pracowników, którzy zarabiali nic mniej niż 1679 tys zł (D\) i nic więcej niż 5091 tys zl (/7_y) pozwala na stwierdzenie, że w tym obszarze zmienności występuje asymetria nieco silniejsza niż poprzednio - można ją określić jako umiarkowaną.

95