dupa0092

Funkcja ma posiać log y, = 1,8767 - 0,545 log x„ a po zdclogarytmowaniu y, = 75,28'.t,'^0,545.

Badamy dopasowanie funkcji do danych empirycznych:

-V,	yi	Pi	y, -Pi	(y, -Pif	y, -Pi	(yi-pf
1	73	75,3	-2,3	5,29	26	676
2	56	51.4	4,6	21,16	9	81
3	40	41,2	-1,2	1,44	-7	49
4	34	35,1	-1,1	1,21	-13	169
5	32	31.1	0.9	0.81	-15	225
15	235	X	X	29.91	0	1200

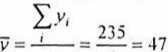
n 5

Odchylenie standardowe składnika resztowego:

Se(V) =

T

n-k

-JM. 3,16 V 5-2

Współczynnik zbieżności:

29,91

1200

= 0.025

Ib-Aj*

9 " ( KV) =    ^ =

' Ifo-aJ*

11. Aproksymujemy funkcję wykładniczą y, = a ■ b^x‘ . Funkcję przekształcamy w postać liniową: logy, = logn + .r, ■ log/;, a następnie wykonujemy obliczenia pomocnicze, niezbędne do zapisania układu równań normalnych (3.55).

X,	Vj	log V,	-r Xj	X, log V',
l	73	1,8633	i	1,8633
2	56	1,7482	4	3.4864
3	40	1,6021	9	4.8063
4	34	1.5315	16	6,1260
5	32	1.5051	25	7.5255
X	X	8.2502	55	23.8175

Obliczamy parametry funkcji:

"Z*,'og^ -MtaWł

log* = -i--f-^-

"YJ - Z^x<

/    \ i /

5>g.v, -logiZ*/

logrt = J-*—

5-23,8173-15-8,2502 5 - 55 — 15²

= -0,0933 ; b = 0,8067

8,2502-(-0,0933)-15

1,9299 ; a = 85,0942

Poszukiwana funkcja ma zatem postać: log jp, = 1,9299 - 0,0933 • x,, a po zdclogarytmowaniu y, =85,09- 0,81*'.

Badamy dopasowanie funkcji do danych empirycznych.

Odchylenie standardowe składnika resztowego:

W

Sc(V) =

n-k

Współczynnik zbieżności:

‘ Z(y. -y.f

<p^: (yx) = -ź

fsl9

~\5~:

: 4,32

55,94

Z (y-Pif ¹²⁰⁰

= 0,047

Xi	y,	Pi	y< -Pi	(vi ~P'f
1	73	68,9	4,1	16,81
2	56	55.8	0.2	0,04
3	40	45.2	-5,2	27,04
4	34	36,6	-2.6	6,76
5	32	29.7	2.3	5.29
15	235	X	X	55.94

Wykonujemy

C. Aproksyinujciny funkcję hipcrboliczną y,=a + b — .

obliczenia pomocnicze do wzorów (3.57).

x,	y,	1 lx,	v,- l/.v,	(I/*,)-
1	73	1,00	73.0	1.000
2	56	0,50	28,0	0,250
3	40	0.33	13,2	0,109
4	34	0,25	8.5	0,063
5	32	0.20	6.4	0.040
X	235	2.28	129.1	1.462

179