fizyka013

ruchów prostoliniowych: ruchu jednostajnego wzdłuż osi Ox ze stałą prędkością v_Qx = v₀ cos a i ruchu jednostajnie zmiennego wzdłuż osi Oy z prędkością początkową v_0y = v₀ sin a i stałym przyspieszeniem a. Pisząc wzór (3.Ib) przyjęto zwrot osi Oy przeciwny niż zwrot wektora przyspieszenia a. Ze wzorów (3.Ib) i (3.2b) wynika, żc po czasie /. ciało osiąga maksymalną wysokość h_t> a po czasie 2t_s wraca do położenia y = 0. Mamy bowiem na podstawie v_y (t_x) = 0, y (t_t) = h.

Zasięg z w rzucie ukośnym jest określony wartością współrzędnej .v dla t = 2/., to znaczy ,v(2/_r) = z, i na podstawie (3.la) wynosi

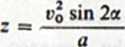
(3.4)

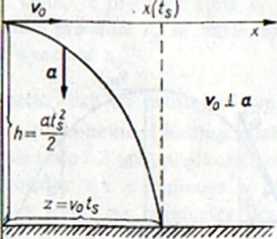
Szczególnym przypadkiem rzutu ukośnego jest rzut poziomy. W tym przypadku wektor e₀ jest prostopadły do wektora przyspieszenia a (rys. 3-2). Kinematyczne równania ruchu dla rzutu poziomego mają postać

(3-5a)

-X (f) = (v₀ cos a) t

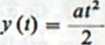
(3.5b>

y

Rys. 3-2

Dla prostoty rozważań na rys. 3-2 kierunek osi Oy wybrano zgodny z kierunkiem wektora przyspieszenia. Ze wzorów dla zasięgu r, liczonego wzdłuż osi Ox, otrzymujemy wyrażenie

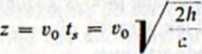
(3.6)

gdzie t_M oznacza czas spadania z wysokości A, liczonej wzdłuż osi Oy (rys. 3-2).

Zadania w tym paragrafie dotyczą ruchu ciał przy rzucie poziomym i ukośnym, zachodzącym w polu sił ciężkości. Pole sił ciężkości jest polem niejednorodnym, gdyż linie sił tego pola nie są do siebie równoległe, lecz zbiegają się w środku masy Ziemi. W zadaniach tego paragrafu będziemy jednak rozważać rzut poziomy lub ukośny o niewielkim zasięgu. W tym przypadku możemy uznać pole grawitacyjne za jednorodne, tzn. za takie, w którym przyspieszenia g są jednakowe w każdym punkcie i są skierowane wzdłuż równoległych linii pionowych. W przypadku ruchu w polu sił ciężkości w kinematycznych równaniach ruchu, danych równaniami (3.1) i (3.5) w układzie odniesienia związanym z Ziemią należy podstawić a = g. Równania (3.1) i (3.5) mają jednak ogólniejszy charakter i mogą opisywać ruch również w innym jednorodnym polu sił.

Rzut ukośny lub poziomy w polu sił ciężkości może być rozpatrywany jako ruch złożony z dwóch niezależnych ruchów: ruchu ciała z prędkością stałą w kierunku poziomym i ruchu jednostajnie zmiennego w kierunku pionowym z przyspieszeniem g. Wyjaśnia to prosty model, który czytelnik może zawsze wykorzystywać przy rozwiązywaniu zadań dotyczących rzutu ukośnego. Niech obserwator A' (rys. 3-3), jadący na platformie poruszającej się z prędkością v_0x po torze płaskim i poziomym w kierunku osi Ox. r/uca do góry piłkę z prędkością r_0r W układzie obserwatora A'

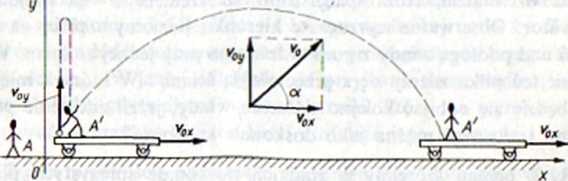
Rys. 3-3

31