HWScan00190

gdzie

x

jednostkowy powierzchniowy opór ścinania, kG/cm², przyjmujemy wstępnie w mechanizmach jazdy

t = C *+- a_n tg o 2 C C — spójność podłoża, kG/cm².

a/

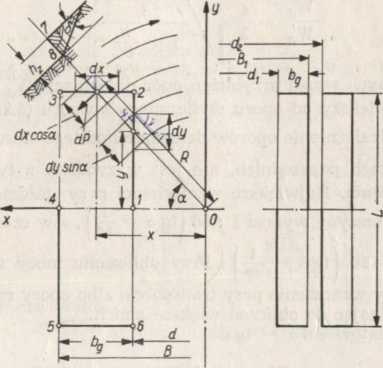
Rys. 5.31. Schemat pracy gąsienic zagłębionych w podłożu

a — wózek dwugąsienicowy, b — wózek czterogąsienicowy

Element długości dy krawędzi 1—2 powoduje w czasie obrotu ścinanie pasa gruntu o szerokości dy sina. Elementarna powierzchnia ścinania dF zależy od wielkości zagłębienia h_z i wynosi

dF = dy sina    -

* smd

gdzie ó oznacza kąt pochylenia płaszczyzny poślizgu przy ścinaniu. Stąd moment konieczny do ścinania krawędzią 1 H- 2 po podstawieniu sina -

= wynosi

^v 2

I dP R —

v—o

sinó

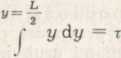
sind

y n

o

y = 0

My 1 + 2

T KL'¹ 8 sin<^

Dla obrotu czterech krawędzi wózka dwugąsienicowego (rys. 5.31 a), tj. l-i-2 i 4-^5 gąsienicy lewej, oraz odpowiednich krawędzi I'h-2' i 4'-f-5' gąsienicy prawej konieczny jest moment

W przypadku obrotu jednej gąsienicy o szerokości B = b_g i długości L, podłoże będzie ścinane tylko przez dwie krawędzie 1-.-2 i 4--5 (rys. 5.32a). Zatem

(5.34)

My ⁼ ^ M_y J+2

ih, L-2 sin<5

(5.33)

th, L²

4 sind

Moment związany z obrotem krawędzi 2-^3 w wózku dwugąsienicowym (rys. 5.32 b) po podstawieniu cosa =    * odpowiednio wynosi

M,

B

^x_ 2

— f rdxcosa    R

2-r- 3    J    smd

_ch_z_ 2 sin b

xdx

r3 =

rh, bg^bg + d) 2 sinó

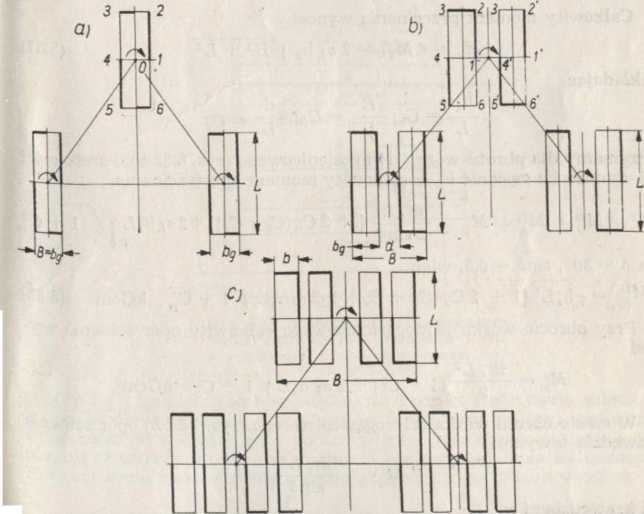
Rys. 5.32. Układy podwozi gąsienicowych zagłębionych w podłożu a — wózek jednogąsienieowy, b — wózek dwugąsienicowy, c — wózek czterogąsienicowy

943