new 85

174 7. Zasady obliczeń wytrzymałościowych śrub

i stąd równanie rozkładu nacisków ma postać

174 7. Zasady obliczeń wytrzymałościowych śrub

pU^x) =

£ Qu

*«= 1

n

£ Qu>idi i-1

F,

X.

(7.127)

n

Równomierny rozkład nacisków istnieje wtedy, gdy V ©„„a, = 0. Wy-

i-l

stępuje to przy symetrycznym rozmieszczeniu śrub o jednakowych przekrojach lub przy niesymetrycznym rozmieszczeniu śrub o odpowiednio dobranych przekrojach.

Zwrócić należy uwagę, że jeśli suma momentów statycznych sił Quh jest mniejsza od zera    Q_w&i < 0 j , to naciski osiągają wartość mini

malną dla x=-^- (punkt K na rys. 7.47a). Wartość ta według równania (7.127) jest ujemna (p_wmin < 0), gdy

Ponieważ

£ Qwi

n

£ Qwiai i-i__a

ly    2

<0.

(7.128)

n    n

£ Qu-,ai = e £ Q_uH    (7.129)

1-1    1 = 1

(gdzie e jest odległością środka ciężkości pól przekrojów śrub od środka styku), więc po podstawieniu równania (7.129) do nierówności (7.128)

n

i uproszczeniu przez VQ_ul otrzymamy 1 = 1

e a 2 I_y

<0.

Stąd jeśli zachodzi nieróiwność

e< -

2 Iy F_s a

' 12 baa

(7.130)

w punkcie K wystąpi luz. Jak z powyższego wynika, dowolne rozmieszczenie śrub prowadzić może do zupełnie niepożądanych konsekwencji.

Zwykle przekroje wszystkich śrub przyjmuje się jednakowe (F, = F), wówczas Qwi = Q_w i równanie (7.127) przy uwzględnieniu (7.119) oraz (7.129) przybiera postać

PA^X)

nF

>7

+

e n F

X I = (Tu;

nF

F.

(7.131)

Obciążenie robocze P przyłożone w środku styku wywołuje równomierne zmniejszenie nacisków na całej powierzchni, a moment M„ (dodatni kierunek momentu przyjęto jako przeciwny do ruchu wskazówek zegara) powoduje zwiększenie nacisków na powierzchni znajdującej się z jednej strony osi symetrii styku (na rys. 7.47a z lewej) i zmniejszenie nacisków na powierzchni po stronie przeciwnej. W sumie liniowozmienne zmniejszenie nacisków jest równe

(7.132)

Dla zapewnienia szczelności styku nacisk resztkowy powinien spełniać warunek

P*(x) = Pu,(x)-p,(x) - _0u, — ■— 1 -+

* t \

(7.133)

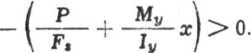
a

Z warunku tego określamy naprężenie wstępne śrub dla x =

P , M„a

---1- ~—

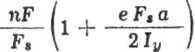
(7.134a)

oraz dla x =--^-(punkt L na rys. 7.47a)

Z

P M_y a

Fs " 2Iy

nF

Fs

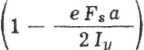
(7.134b)

Miarodajne jest większe spośród naprężeń określonych wzorami (7.134a) i (7.134b).

Przy powszechnie stosowanym, symetrycznym rozmieszczeniu śrub (e = 0) równanie (7.134a) sprowadza się do postaci

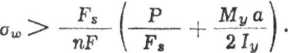
(7.135)

Dla styku jak na rys. 7.47b równanie nacisków wywołanych napięciem wstępnym ma postać

Pw{x, y) = A + Bx+Cy.

(7.136)