3582308527
ALGEBRA LINIOWA - macierze, wyznaczniki, układy równań liniowych.
24. Macierze - definicja, rodzaje własności, działania na macierzach, iloczyn tensorowy (w sensie Kraneckera), iloczyn macirzy (Cauchy’ega), wykonalność mnożenia
Macierz prostokątna - Jeżeli m,n sąustalonymi liczbami naturalnymi i M={l,...,m}, N={1.....N} to X=MxN.
Oraz weźmy niepusty zbiór Y i określimy funkcję f:X-»Y (feFim(X,Y)). Macierząprostakątnąnazywamy funcję f z m - wierszami i n - kolumnami przyjmującąwartości w zbiorze Y.
|
fu |
f 12 |
- fis, | |
|
f [fj.k]j=LiP, k=l1D |
f21 |
f22 |
f2n |
|
_ fml |
fm 2 |
" fmn_ |
Macierz transportowana F=[fkj]k=in,j=Lm - jest to macierz otrzymana z macierzy f przez zamianę wierszy na kolumny i kolumn na wiersze.
Wymiar macierzy - Jeśli macierz A ma m- wierszy i n- kolumn to macierz jest rozmiaru m x n.
Wymiar macierzy tr anspanowanej AT wynosi n x m. Jeśli ilość kolumn jest równa ilości wierszy n to wymiar macierzy jest n x n i taką macierz nazywamy macierz ą kwadratową.
Suma macierzy -
A-[ aalFtig. ł=Lp i B-f bltli^i.m. t=Lo A+3-C— [ CflL-l.ni. t-i.p gdzie C§— ag^bif t=Lm. Vln
np.:
|
'°U |
a!2 |
" ain~ |
~bu |
b12 |
•• K' | ||
|
A = |
a21 |
a22 |
" a2n |
i B = |
b21 |
b22 |
" b2n |
|
.°ml |
°m2 ' |
" ®mn _ |
bml |
bm2 |
to
an + bn °21 + b21
ai2 + b12
a22 + ^22
ais,+bis,
a2n+b2n
A + B =
a„„ +bmn
mn mn _
_a«i + bmi
am2 + bm2
Iloczyn macierzy przez liczbę - c*A=[c*
|
~an |
°12 |
" Qln’ |
~c*au |
c*au . |
" C*ain_ | ||
|
nn: A = |
a21 |
°22 • |
" Q2„ |
to C * A = |
c*a21 |
C*Q22 • |
" C*Q2„ |
|
.°ml |
am2 ■ |
•• ®mn _ |
C*am2 • |
- C*Q™_ |
Iloczyn tensorowy (w sensie Kraneckera)
A~[ t=1.n i B-[ bl, li ii p i-i.r
ASB—IflaSH Fią
np:
|
au |
Q12 |
Q13 | |
|
A = |
Q21 |
0.^2 |
°23 |
|
_a31 |
°32 |
Q33_ |
oraz
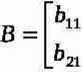
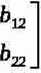
Wyszukiwarka
Podobne podstrony:
47137 MATEMATYKA188 366 vn Macierze. Wyznaczniki. Układy równań liniowych (24) allxl a2lxl + a„x2 +
s108 109 3. MACIERZE, WYZNACZNIKI I UKŁADY RÓWNAŃ LINIOWYCH3.1. Działania na macierzach 1. Dane są
MATEMATYKA179 348 VII Macierze Wyznaczniki Układy równań liniowych --— x aII. ai2 at3, a2ly. a22,
MATEMATYKA183 356 VII. Macierze. Wyznaczniki. Układy równań liniowych kolumny tworzymy minory drugie
MATEMATYKA184 358 vn Macierze. Wyznaczniki. Układy równań liniowych ZADANIA DO ROZWIĄZANIA 0 0 0 0 0
20944 MATEMATYKA186 362 VII. Macierze. Wyznaczniki. Układy równań liniowychw, w2 wn _ a,,x,+a,2x2+ .
22064 MATEMATYKA189 368 Vn. Macierze. Wyznaczniki. Układy równań liniowych 368 Vn. Macierze. Wyznacz
więcej podobnych podstron