3582316268

ANALIZA MATEMATYCZNA 2

Zestaw

WEMiF, II kolokwium, 10 czerwca 2011 r.

1. Znaleźć wszystkie ekstrema funkcji

Rozwiązanie. Oczywiście y ^ O Z warunku koniecznego istnienia ekstremum mamy

3x

= -l(|+l)=0,

J4 = -2(_#-4)+2(j+l)^=0.

Z pierwszego równania wynika, że - +1 =0 Po wstawieniu tej równości do drugiego równania,

y

otrzymamy y = 4 i stąd x = —4. Bozwiązaniem układu równań jest zatem para:

»i = -4,

yi = 4

Przechodzimy do warunku wystarczającego istnienia ekstremów. Mamy

a¹/    2

as:'

a¹/    a¹/ _ 4a-t-2y

a^ay    a^a* y³ 1

d²f _    2(3«¹+2ay+j/³')

3F -    —?-*

Badamy znak hessjanu w punkcie „podejrzanym o ekstremum”. Mamy

S(^-4’³) S(^-4’³)

i

&xBy

£&(-«. 4)    0<-4,4)

Zatem jest to maksimum lokalne właściwe.

i? (-4,4) = det

det

i

' 8

17

8

> 0

1

1

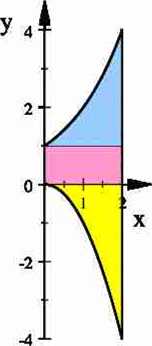
Narysować obszar całkowania i następnie zmienić kolejność całkowania w całce iterowanej

2 2®

2

jdx J /(»>»)

3

Rozwiązanie. Obszar całkowania przedstawiamy na rysunku poniżej: