3582320341

ANALIZA - ZESTAW nr 8 (WMS, rok 1, gr. 4, sem. letni 2011-2012)

1. Obliczyć granice:

a)

*)

c)

d)

e)

i:    a:² - y².

•Um    rj    rj J

(z,v)-+(0,0) x² 4- y²

i-    ,    , .    1 .    1

lim    [x + y) sin — sm

(*,v)-Ko,o)    x y

lim

lim

x²y

x² 4-y²

(x,v)-Ąo,o) y/x² 4- y² 4-1 — 1⁵ ^ sin (x¹ 4- y¹) _ (*,v)->(o,o) X² 4- y²

/)

ęxⁱ+y‘^J

lim —j--

(z,v)-Ko,o) X⁴ + y⁴

2. Niech

^nx'^v) = xvl(z-_vr

Pokazać, że granice iterowane

lim (lim f(x, y) j , lim (lim f(x, y))

z-fO \v-40 ^v '/    K-40 \z-40    '    )

istnieją i są równe 0, ale nie istnieje granica

lim

(z,V)-4(0,0)

lim

(a; 4- y) sin — sin x

1

y

ale nie istnieją granice iterowane

lim

z->0

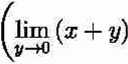
sm

— sin — ) , lim (lim (x 4- y) sin -x y) v-+o yz-i-o    z

. 1 sm -

y

1

Wykazać, że istnieje granica