1636661680

11

2. METODA SYMPLEKSOWA

Jeśli zbiór X jest domknięty i ograniczony, to dowolny punkt tego zbioru może być przedstawiony jako wypukła kombinacja punktów ekstremalnych. Wektor 0 ^ v G Mⁿ nazywamy kierunkowym zbioru X, jeśli

VxexV\>o x + \v E X.

Dwa wektory kierunkowe u, w zbioru X nazywamy równymi, jeśli

3a>o v = Aw.

Wektor kierunkowy v zbioru X nazywamy ekstremalnym, jeżeli

V«,_1iW2Va₁,a₂>o v - XiWi + A₂w₂ =>• 3_a>o^i - Aw₂,

gdzie wi,W2 są wektorami kierunkowymi zbiory X.

W dalszej części rozważać będziemy zbiory X postaci I = {rG Rⁿ; Ax = b,x > 0}, gdzie A oznacza macierz wymiaru m x n, b G M^m. Zakładamy ponadto, że vz(A) = m. Niech A = [J3iV] (po ewentualnej permutacji kolumn), gdzie B jest m x m macierzą, N jest m x (n — m) macierzą, natomiast rz (B) — m. Wtedy

Ax = b, x > 0 => Bxb + Nxn = b,

gdzie xb > 0,    > 0. Niech A będzie jak wyżej. Wówczas przez C(A) ozna

czamy zbiór takich macierzy nieosobliwych B wymiaru m x m, dla których istnieje macierz N wymiaru m x (n — m) taka, że [j37V] da się uzyskać z macierzy A poprzez przestawienie kolumn.

Uwaga 2.5. Dalej będziemy stosować następujące uproszczenia notacji. Zapis A = [BN] będzie oznaczać, że macierz A można uzyskać z macierzy [BN] przez pewną permutację a kolumn. Wtedy x = [x_Bx_N] będzie znaczyć, że wektor x powstaje z wektora x = [xbXn] przez tę samą permutację a współrzędnych.

Twierdzenie 2.6 (o charakteryzacji punktów ekstremalnych). Niech X = {x G Mⁿ; Ac = 6, x > 0}, gdzie A G M_mxn(M), b G rz(A) = m. Punkt

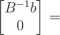
x G X jest punktem ekstremalnym wtedy i tylko wtedy, gdy x =

^Xb dla pewnego B G C(A) takiego, że B^_1b > 0.