79573326

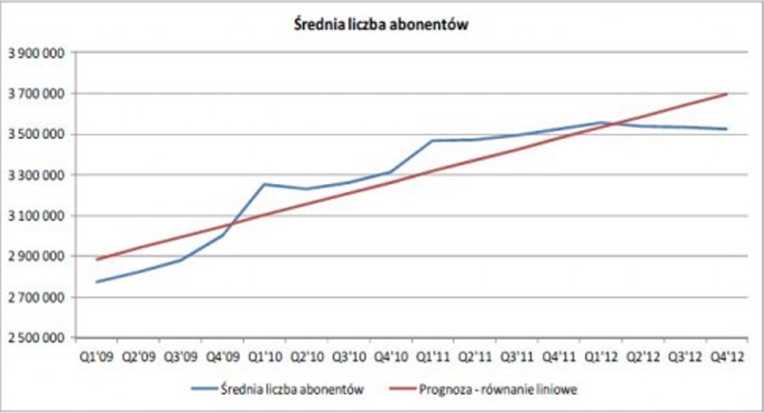
modeł regresji: y = 53.998 * x + 2.831.003
Trend - równanie	Odchylenie	Odchylenie
liniowe	liczba abonentów	%
8	C * B - A	C/A
2 885 002	109 525	3,9%
2 939 001	118 192	4,2%
2 993 000	114 153	4,0%
3 046 998	43 427	1.4%
3 100 997	-150 521	4,6%
3 154 996	74 503	-2,3%
3 208 994	50 734	1,6%
3 262 993	51884	-1,6%
3 316 992	-149 109	4,3%
3 370 990	101 720	-2.9%
3 424 989	68 135	2.0%
3 478 988	44 215	1,3%
3 532 986	-21 889	-0,6%
3 586 985	48 544	1.4%
3 640 984	109 954	3.1%
3 694 982	168 914	4.8%

dane historyczne
Nr	Kwartał	Średnia liczba
		abonentów
		A
1	Q1'09	2 775 477
2	02'09	2 820 809
3	Q3'09	2 878 847
4	Q4’09	3 003 571
5	Q110	3 251 518
6	Q2'10	3 229 499
7	Q3'10	3 259 728
8	0410	3 314 877
9	Ql'll	3 466 101
10	Q2'll	3 472 710
11	Q3'll	3 493 124
12	Q4'll	3 523 203
13	Q1'12	3 554 875
14	Q2'12	3 538 441
15	Q3'12	3 531030
16	Q4'12	3 526 068