17150

2

PODSTAWY KOMBINATORYKI

Symbol "!" nazywany jest silnią, a symbol (£) symbolem Newtona. Definicję .syml>olu Newtona można rozszerzyć, pozwalając, by liczba « w (J!) była liczbą rzeczywistą (lub nawet zespołemą), definiując:

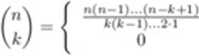
dla k > 0, dla k < 0.

O)

Zauważmy, że w przytułku uogólnionego symbolu Newtona (JJ) = 1 tylko dla n > 0. Dla n < 0 mamy (") = 0.

Metoda ustalania hijekcji. Jeśli mamy zliczyć ilość elementów jakiegoś zbioru A', ale |K>lk:zenk? ich wprost nie jest łatwe i nie da się bezpośrednio zastosować pod-stawowych wzorów kombinatorycznych, można wtedy użyć tzw. metody ustalania bijckcji. Polega ona na ustaleniu bijektywnego odwzorowania pomiędzy elementami, które mamy policzyć, a elementami zbioru Y. którego elementy da się już zliczyć w łatwy sposób. Jeśli uda się pokazać, że taka bijekcja istnieje, oznacza to. że liczność zbioru X jest równa liczności zbioru Y.

ZADANIA

Zadanie 1. Ile jest wszystkich funkcji / : X -*Y. gdzie |A| = k > 0, |K| = n > 0?

Zadanie 2. Ile jest wszystkich funkcji różnowartościowych f : X —* Y, gdzie |Aj = k > 0, \Y\ = n > 0?

Zadanie 3. Ile jest przekątnych w n-kącie foremnym?

Zadanie 4. Na ik* sposobów’ można wybrać k > 0 elementów z n-elementowego zbioru, n > 0, jeśli kolejność wybranydi elementów* nie ma znaczenia i wybrane elementy mogą się powtarzać?

Zadanie 5. Ile jest funkcji nkunalejących ze zbioru ^-elementowego w zbiór n-elementowy, k, n > 0?

Zadanie 6. Na ile sposolrów można rozmieścić k > 0 rozróżnialnych kul w n > 0 rozróżnialnydi pudelkach, jeśli pudełka zawierają uporządkowane ciągi elementów (dopuszczamy ciągi puste)?

Zadanie 7. Ile jest ciągów' binarnych o długości n > 0?

Zadanie 8. Ile jest wszystkich podzbiorów zbioru n-elementowego. n > 0?

Zadanie 9. Na ile sposol)ów można zapisać w jednym rzędzie cyfry 0. 1.....9 tak.

by 8 i 9 stały olx>k siebie?

Zadanie 10. Na ile sposobów można posadzić przy okrągłym stole n > 0 osób?

Zadanie 11. Ile jest kostek domina w zestawie, w* którym oczka na polówkadi kostek domina mogą przyjmować w*artości 0, 1.2. 3, 4, 5, 6?

Zadanie 12. He jest różnych rozdań w brydżu?

Zadanie 13. Jakie jest prawckąiodobicństwo, że w^f 30-osobowej grupie ćwiczeniowej istnieją dwie osoby olxhodzące urodziny w tym samym dniu?