23203

MODEL BROWNA

Jest to prosty model wygładzania wykładniczego szeregu czasowego. Zwykle może być stosowany w przypadku gdy w danym szeregu występuje prawie stały, umiarkowany poziom zmiennej prognozowanej oraz wahań przypadkowych.

W modelu tym wyznaczenia prognozy na okres t lub t-1 dokonujemy na podstawie wzorów:

_ .v, ,	*
i	St-1 f
	••+ X-*-.

y t - prognoza zmiennej y wyznaczona na moment lub okres

y_f.i-wartość zmiennej prognozowanej w momencie lub okresie t-1

k -stała wygładzania

Jednak gdy wartość zmiennej prognozowanej wyznaczonej na moment lub okres t-k-1 zastąpimy wartością przybliżoną wartości prognozy wyznaczonej na poprzedni moment lub okres, wzór ma postać:

y

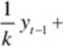
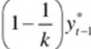
Poprzez taki zabieg powstało nam równanie, w którym obserwacji zmiennej prognozowanej przypisana jest waga 1/k, a prognozie l-(l/k). Wagę tą możemy zastąpić symbolem a, wtedy równanie ma postać:

y’ = °v,-\+0-«).v*-i

Model Browna jest rozwinięciem metody średnich ważonych co oznacza, że wagi maleją wykładniczo przy coraz starszych danych. Łatwo można to zauważyć gdy przekształcimy wyżej przedstawiony wzór podstawiając y*__x = ocy,_₂ + (l — cc)y*_₂ otrzymamy:

y, = «y,-i + (1 - a \ay,_₂ + (l - a )>>,*_₂):= ary,., + a( I - a )y,_₂ + (l - a f y'_l 2

Kroki te możemy powtarzać w zależności od ilości okresów t. Ostateczny wzór ma postać:

y' =<xy,-1 + a(l - a )y,_₂ +... + a(l-af y,._k„ +...

W modelu tym za wartość y, przeważnie przyjmuje się wartość początkową zmiennej prognozowanej lub średnią arytmetyczną rzeczywistych wartości zmiennej prognozowanej z próbki wstępnej.

Wartość parametru o zazwyczaj dobiera się eksperymentalnie poprzez konstrukcję na podstawie próbki wstępnej prognozy dla różnych wartości a i wybiera się tę wartość, przy której średni błąd prognoz był najmniejszy. Wartość tego parametru wygładzania zawiera się w przedziale zamkniętym między 0 a 1 —> / ae(0,l] /