23384

Punkty skupienia ciągu

Definicja

Ciąg (b_k)_ttK nazywamy podciągiem ciągu (a„)»eN , jeżeli istnieje taka silnie rosnąca funkcja g:IN-*M , że b_i=a_g{ll dla keN i oznaczamy b_k=a_n(ll=a„ .

Przykład

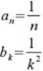
(^OweH*

jest podciągiem (a„)„_6N , bo funkcja wybierająca g(i)=A^; jest silnie

rosnąca.

Definicja

Niech ¥ - przestrzeń topologiczna lub metryczna,

Punkt sey nazywamy punktem skupienia ciągu («„)„«=« , jeśli istnieje taki podciąg ciągu (a„)„_6N , że *=lim a„ .

Oznaczenie

'(⁰»)mn -zbiór punktów skupienia ciągu («„)„_en

Uwaga

Zbiór punktów skupienia ciągu wartości ciągu,

(fl.La, jest różny od zbioru punktów skupienia zbioru

'("»Ln * ’ <i„,»eiN

Przykład

Niech <i„=(—1 )", neM Wtedy

dla b_k = a_2k -1 limfc_ł=l oraz dla c, = a,,_,=-l lim c_t= — 1

Zatem '(«„)=[ —1 ,1 ;

Jednak '[a„, «eN]='(-l, 1 ; = 0 w R