24437

e,' = e, + e,

ej¹ = ej + e, + ej Sprawdzamy, ze Bjjest bazą: aej'+ fie,'+ /ej' = O

aej + /?(ej + e₂)+y(e, + e₂ + ej) = O (a+p + y)e,+(p+y)e,+(y)e₃ = Ó ej,e₂,ej - wektory liniowo niezależne

a+p+y=0	f«=o
P + y = 0	=>\p = Q
O II	[/ = 0

i dimX=3, więc B' jest bazą

e,' = le, + 0e2 + 0e3 = [l, 0,0]B		1 1 1
e, '= lej + le, + Oej = [l.l,0]s	P =	0 1 1
e,' = lej + le, + lej = [l. 1, l]fi		O O

WNIOSEK

1)    macierz P jest macierzą nieosobliwą P_B->B' oraz    jest macierzą

odwrotną

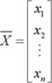
2)    x = [x„x,,...,x„]_fl = [x, ^,,x₂^,,...,a:„']_b *1

Na podstawie postaci macierzowej: X = P X'^> X' = P ¹ X

Przykład 1'.

x = ej - 2e, + 3ej = [l, -2,3]_s = [x, x,x, ']_s.©

' 1 -2	_	i i r 0 1 1	V x2'		X, ’+x2'+xi'= 1 x2'+ x3^1 = -2
3		o o	.V.		Xj' = 3

©[3.-5,3]_s.

Wykład dr Magdaleny Sękowskiej strona 2 z 5 Część 8 - Zmiana bazy