26193

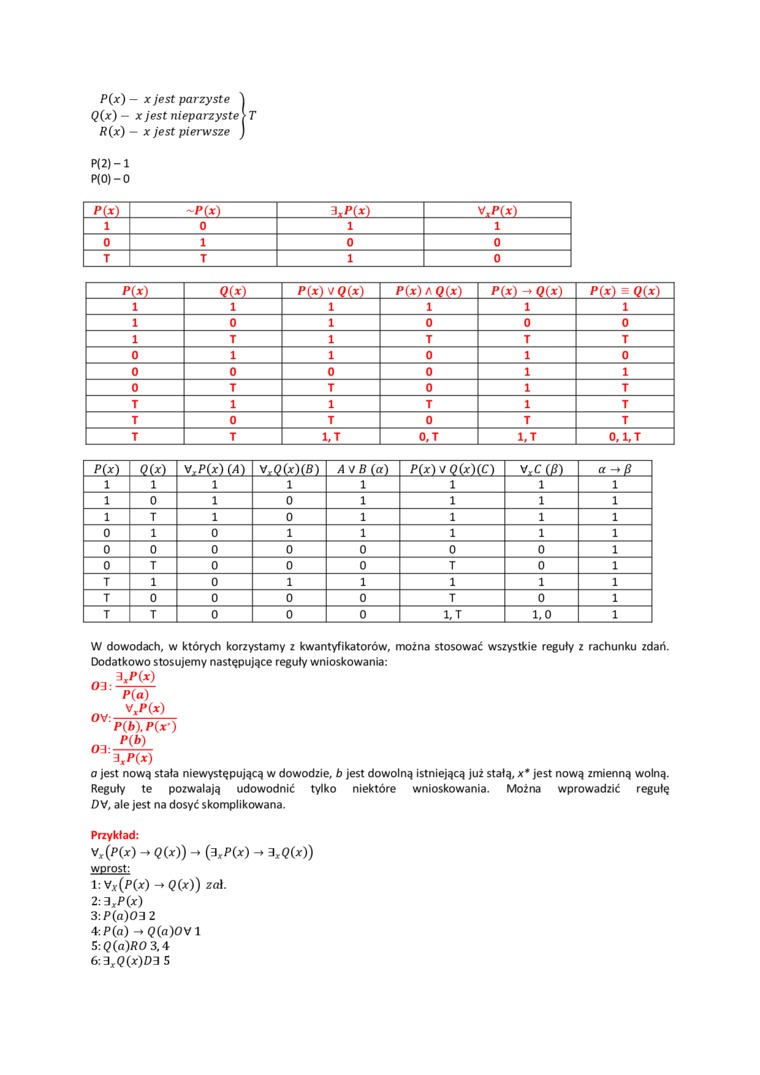
P(x) - x jest parzyste ) QM - x jest nieparzyste > T RM - x jest pierwsze J

P(2)-l

P(0)-0

W dowodach, w których korzystamy z kwantyfikatorów, można stosować wszystkie reguły z rachunku zdań. Dodatkowo stosujemy następujące reguły wnioskowania:

3 _XPM

03:

0V:

03:

P(«)

V,PQO

P(b).PM)

P(b)

3_xP(x)

a jest nową stała niewystępującą w dowodzie, b jest dowolną istniejącą już stałą, x* jest nową zmienną wolną. Reguły te pozwalają udowodnić tylko niektóre wnioskowania. Można wprowadzić regułę DV, ale jest na dosyć skomplikowana.

P(x)	-PM	3 rPM	v,P(*)
1	0	1	1
0	i	0	0
T	T	1	0

PM	<?(*)	P(X)V<?(X)	P(*)A<?(X)	PM - QM	PM = QM
i	1	1	1	i	i
i	0	1	0	0	0
i	T	1	T	T	T
0	1	1	0	1	0
0	0	0	0	1	1
0	T	T	0	1	T
T	1	1	T	1	T
T	0	T	0	T	T
T	T	1, T	0, T	1, T	0,1,T

PM	QM	V,P(x) 04)	v,<2C0(fi)	A V B (a)	P(*)v <2(x)(C)		a -* /?
l	l	1	i	1	l	i	1
1	0	1	0	1	i	i	1
i	T	1	0	1	i	i	1
0	1	0	1	1	i	i	1
0	0	0	0	0	0	0	1
0	T	0	0	0	T	0	1
T	1	0	1	1	1	1	1
T	0	0	0	0	T	0	1
T	T	0	0	0	1, T	1,0	1

Przykład:

v,(PM -* <?(*))    (5,PW -» 3,<?w)

wprost:

1: V_x(P(x) -*Q(x)) zal.

2:3 _xP(x)

3:P(a)03 2 4:P(a) ->Q(a)OV 1 5: Q(a)RO 3,4 6:3_rQ(x)D3 5