34520

6.2. Momenty bezwładności układu punktów materialnych

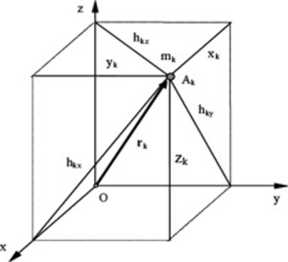
Rys. 6.1. Opis położenia punktu materialnego

Załóżmy, że mamy układ materialny złożony z n punktów materialnych o masach m* znaj dujący cli się w punktach Ak opisanych wektorami wodzącymi r_fc (rys. 6.1).

r_k = x_k ł+ y_k j+ zk

Biegunowym momentem bezwładności I_Q układu punktów materialnych względem punktu O nazywamy sumę iloczynów mas nt i kwadratów ich odległości r_k² od punktu 0, czyli

n

i₀=S^mk^rk =y,ⁿ\(*l ⁺ yl^+zi) •

k-i

(6.1)

Momentalni bezwładności I^. I_y7. 1^ wzglądem płaszczyzn xy. yz. zx układu piuiklów materialnych nazywamy sumy iloczynów mas m_k przez kwadraty ich odległości od tych płaszczyzn. Zatem mamy:

^Iyz=X¹«k^Xk’ ^Izx = X^lllkyk² •    (⁶²)

k-l    k-l    k-l

Momentami bezwładności I_x, I_y. I_z wzglądem osi X. y, z układu punktów mateiialnych nazywamy sumy iloczynów mas m* oraz kwadratów icli odległości od tych osi:

k-l    k-l

(6.3)

I_r = Vni_th^ = Vnv(z; + xj} ■

k-l    k-l

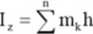
2 kz

k-l

£>_k(x_k²+y_k²)

Oprócz zdefiniowanych wyżej momentów bezwładności względem punktu, płaszczyzn i osi w dynamice ważną rolę odgrywają wielkości, które nazywamy momentami dewiacyjnymi (albo momentami mieszanymi lub odśrodkowymi).