36620

Temat- Rozkład Gaussa i Poissona Wstęp teoretyczny

ROZKŁAD GAUSSA: (normalny): rozkład zmiennej losowej (rozkład prawdopodobieństwa) opisany funkcją (tzw. unormowana funkcja Gaussa)gęstości prawdopodobieństwa, w przypadku jednowymiarowym daną wzorem:

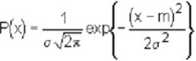
Czynnik przed eksponentą (funkcja eksponencjalna) normalizuje pole powierzchni pod krzywą do jedności, co wyraża oczywisty fakt, że prawdopodobieństwo by zmienna losowa x przyjęła dowolną wartość wynosi jeden.Funkcję Gaussa opisującą rozkład nazywa się czasem funkcją dzwonową, ze względu na kształt wykresu. Istnieją uogólnienia rozkładu Gaussa dla przypadków wielowymiarowych zmiennych losowych. W przypadku o = 0 funkcja Gaussa staje się deltą Diraca.

ROZKŁAD POISONA: jest jednym z rozkładów zmiennej losowej ciągłej. Jest to rozkład asymetryczny. Nazwę wziął od nazwiska osoby, która go wprowadziła. Był to Simeon-Denis Poisson I opisał ten rozkład w swoim dziele: "Procedes des Ragles Generales du Calcul des Probabilltes. Bachelier, Imprimeur-Ubraire pour les Mathematlques", wydanym w Paryżu w 1837. Rozkład Poissona jest przybliżeniem rozkładu dwumianowego dla dużej próby oraz małego prawdopodobieństwa sukcesu.

Mówimy, że zmienna losowa X ma rozkład Poissona z parametrem A > 0, jeżeli zbiorem jej wartości jest {0,1,2,...} oraz

P_k = P(X = k)=£_e-*

•    gdzie:

•    k=0,l,2,... - liczba otrzymanych sukcesów ■ A = E(X) = Z?² = np - wartość oczekiwana

Przyjmując oznaczenia z rozkładu dwumianowego można to zapisać równoznacznie:

gdzie:

n - liczba doświadczeń, przyjmująca duże wartości dla rozkładu Poissona p - prawdopodobieństwo sukcesu