32384

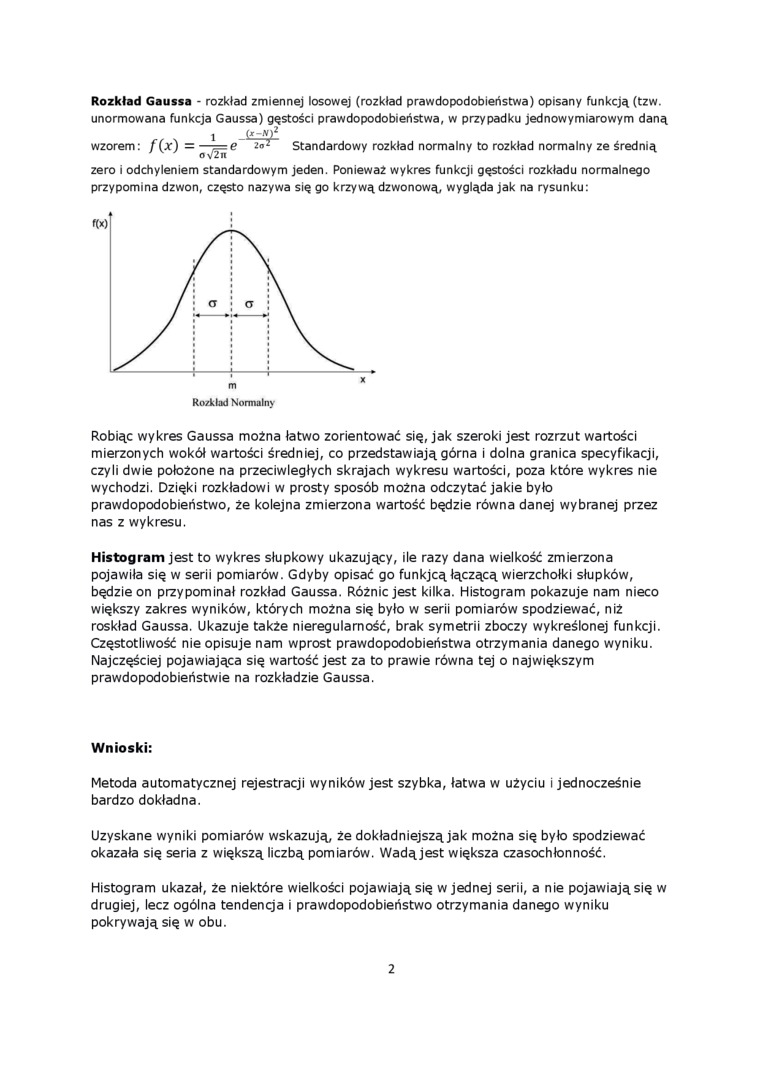
Rozkład Gaussa - rozkład zmiennej losowej (rozkład prawdopodobieństwa) opisany funkcją (tzw. unormowana funkcja Gaussa) gęstości prawdopodobieństwa, w przypadku jednowymiarowym daną

i

wzorem: f(x) = —T=e 2«² Standardowy rozkład normalny to rozkład normalny ze średnią

o v 2n

zero i odchyleniem standardowym jeden. Ponieważ wykres funkcji gęstości rozkładu normalnego przypomina dzwon, często nazywa się go krzywą dzwonową, wygląda jak na rysunku:

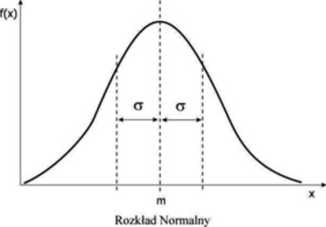
Robiąc wykres Gaussa można łatwo zorientować się, jak szeroki jest rozrzut wartości mierzonych wokół wartości średniej, co przedstawiają górna i dolna granica specyfikacji, czyli dwie położone na przeciwległych skrajach wykresu wartości, poza które wykres nie wychodzi. Dzięki rozkładowi w prosty sposób można odczytać jakie było prawdopodobieństwo, że kolejna zmierzona wartość będzie równa danej wybranej przez nas z wykresu.

Histogram jest to wykres słupkowy ukazujący, ile razy dana wielkość zmierzona pojawiła się w serii pomiarów. Gdyby opisać go funkjcą łączącą wierzchołki słupków, będzie on przypominał rozkład Gaussa. Różnic jest kilka. Histogram pokazuje nam nieco większy zakres wyników, których można się było w serii pomiarów spodziewać, niż roskład Gaussa. Ukazuje także nieregularność, brak symetrii zboczy wykreślonej funkcji. Częstotliwość nie opisuje nam wprost prawdopodobieństwa otrzymania danego wyniku. Najczęściej pojawiająca się wartość jest za to prawie równa tej o największym prawdopodobieństwie na rozkładzie Gaussa.

Wnioski:

Metoda automatycznej rejestracji wyników jest szybka, łatwa w użyciu i jednocześnie bardzo dokładna.

Uzyskane wyniki pomiarów wskazują, że dokładniejszą jak można się było spodziewać okazała się seria z większą liczbą pomiarów. Wadą jest większa czasochłonność.

Histogram ukazał, że niektóre wielkości pojawiają się w jednej serii, a nie pojawiają się w drugiej, lecz ogólna tendencja i prawdopodobieństwo otrzymania danego wyniku pokrywają się w obu.

2