38505

Zadania z egzaminu w sesji podstawowej i poprawkowej po sein.02

Czern iec 2009:

1. a) Obliczyć długość luku krzywej y- ln.r dla *€ (1,2)

b) Obliczyć całkę | tgxdx

X

*2

1	1	0		1	1 1
0 1		1	i B-.	1	0 1
1	1	-1		2i	4 i

2. Rozwiązać równanie macierzowe (AXB) ¹ = A, gdzie A -

3. Dane są punkty: ^4(1,1,1), 5(1,- 1,- 1). C(2,0,2). D(- 1,1,0) .

a)    Pizy pomocy rachunku wektorowego obliczyć objętość czworościanu ABCD i pole Ściany ABC

b)    Napisać równanie płaszczyzny przechodzącej przez punkt C i równoległej do ściany ABD

Obliczyć odległość punktu A od płaszczyzny.

r (- 1)"

4 Znaleźć przedział zbieżności szeregu: ) -

o w + 99

5.    Znaleźć wartość najmniejszą i wartość największą funkcji: f(x>y) = e²*[y² - x²1 w zbiorze D = {(.t,_v) : v2 0,,v^ 2.r+ 2,x< 0)

6.    Znaleźć ekstrema lokalne funkcji v = /(*)uwikłanej równaniem : .t³ + v³ - 8.rv = 0

(x-2V

Wrzesień 2009:

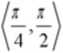
1.

3.

4

5.

6.

a) Obliczyć objętość bryły powstałej przez obrót luku krzywej v = cos 2x dla xe wokół osi OX

i

b)Obliczyć całkę [ ln xdx

Rozwiązać układ równań metodą macierzy odwrotnej

x	y	+	3 r =	1
3x ł	y	ł	2z =	2
2x ł	2v	+	- =	3

Patrz zadanie nr 3 z czerwca a) pole ściany ABD b) D i równoległej do ściany ABC

Odległość od punktu B

Znaleźć przedział zbieżności szeregu £    _f

»o ^w+ 99 \

Wyznaczyć ekstrema lokahie ftuikcji f(x,y) = xy² - .t² v+ 5y Patrz zadanie nr 6 z czerwca

(-2)"/*- 2V