5140

Jednak te przypadki nie wchodzą w zakres sylogistyki, ponieważ nie zajmuje się ona zbiorem pustym, ani uniwersum - nieskończoną ilością elementów.

Klasyczna definicja prawdy /Arystoteles/ „wypowiedź prawdziwa to wypowiedź zgodna z rzeczywistości^’ (teoria poznania)

Prawdziwość zdania zależy od stosunków jakie panują pomiędzy podmiotem a orzecznikiem. Musi to mieć odniesienie do rzeczywistości.

Możemy rozważać jakie stosunki zachodzą między nazwą ogólną a zakresami - a to zależy od desygnatów.

JŁ

	*
0	**

li

indywidua

Całość to uniwersum świata mowy P - zbiór ptaków -i nazwy S - zbiór sów J ogólne * - gil, jest ptakiem i nie jest sową ** - sowa, jest ptakiem i jest sową *** - dąb Bartek, nie jest ptakiem i nie jest sową J 0 - nie ma rzeczy, która jest sową a nie jest ptakiem

Przegląd stosunków ( wszystkie możliwe stosunki przy założeniu, że nie ma zakresów pustych i uniwersalnych)_

zakres bez desygnat □ zakres z desygnatami

Stosunek zamienności a - wszystkie sowy są ptakami i na odwrót

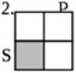
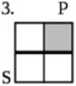
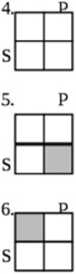
P

Stosunek podrzędności ( S względem P) P - całość zakresu S mieści się w zakresie P ale go nie wyczerpuje.

Stosunek nadrzędności ( S względem P) y - całość zakresu P mieści się w zakresie S ale go nie wyczerpuje

Stosunek krzyżowania 8 - w każdym zakresie są jakieś elementy

Stosunek wykluczania £ - zakres S i P nie mają elementów wspólnych

Stosunek wyczerpywania V - albo należy do S albo do P

Stosunek dopełniania £ - elementy albo nie należą do S ani do P, ale należą do obu zakresów naraz

7.