9878

Matematyka - Liczby zespolone i funkcja zmiennej zespolonej

jzj =sin <p z ^|z|cos^9-ł-f|z|sin t/>=\z\(,co&4/>-t-i -sin </$

4. Potęga, wzory MOIVRE'a.

4.1 Własności modułu i argumentu liczby zespolonej.

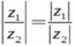
arg(z_Iz₂) = argz,+argz₂

^zi

arg-^L = argz₁ -argz₂ ^Z2

z, = r, (cos a + i sin a)    a=arg z, r, =jz, |

z₂ = r₂(cos/? + /siny?)    (3 = argz₂ r₂ =|z₂|

z, • ^z2 ⁼ • r^[( cos cz cos f3 — sin er sin y?) + /(coscz sin y? + sin cc cosy?)] =

r, • r₂(cos|a + /?) + isinfar + /?))

z" =|z|ⁿ(cos(/i^j) -ł-/sin(n^)

cos2^>=cos² ę>—sin² <p

sin 2<p=2 sin <pcos <p

5. Pierwiastek liczby zespolonej.

Założenie: z" —|zf(cos(n<3j -+-/sin(n<3j) z"=C

C = £|cos(ę> + 2WI) + tsin(ę>+2kn)J

2=VC

W"-«

ne=y+2fcn e=^^l+2lin k = 0,1, 2,..., n-1.

n

/ ! cos

ę> + 2/tfl ^ . . 0 + 2JJ1 Y\

--— 1+ istni--— 11, dla k=0 pierwiastek główny.

6. Postać wykładnicza liczby zespolonej (EULER'a).

e^v =cos<p+isln<p C =e‘ = e^X4,ty = e*(cosę>+/sinę>)

C ==^C|(cos t/>+4 sin «/}

|C| =e* =R

c =\C\e^l4p 0 < <p<2Y\    . postać wykładnicza liczby zespolonej.

C" HC|"e'-

Korzystając z postaci wykładniczej obliczyć

-2-