52937 str028 (5)

28 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

(4.10)

_e2 + 2*!ti _ _gZ ^

(4.11)

sin (z + 2/ar) = sin z, cos(z+2/cit) = cos z,

gdzie k = 0, ±1, ±2, ...

Wzór (4.10) orzeka, że e^z jest funkcją okresową o okresie urojonym 2ni, wzory zaś (4.11) stwierdzają, że funkcje sinz i cosz są funkcjami okresowymi o okresie rzeczywistym 2jt.

Każdą liczbę zespoloną z możemy przedstawić w postaci

(4.12)

gdzie r oraz 0 oznaczają moduł i argument liczby z. Postać (4.12) nazywamy postacią wykładniczą liczby zespolonej.

Logarytmem naturalnym liczby zespolonej z # 0, który oznaczać będziemy symbolem lnz, nazywamy każdą liczbę w spełniającą równość

Twierdzenie 2. Każda liczba zespolona z ^ 0 ma nieskończenie wiele logarytmów naturalnych. Określone są one następującym wzorem:

(4.13)

lnz = ln r+ i0_o + 2kni, k — 0, ±1, ±2,...,

gdzie r oznacza moduł liczby logarytmowanej, zaś 0_o — argument główny liczby logarytmo-wanej 0^0_o<2n.

Logarytm główny z liczby z ^ 0, który oznaczać będziemy symbolem Lnz, określony jest wzorem

Ln z = ln r + i0_o,

gdzie r oraz 0_o oznaczają odpowiednio moduł i argument główny liczby logarytmowanej z.

Każda więc liczba zespolona z ^ 0 ma jeden logarytm główny.

Zadanie 4.1. Znaleźć promień zbieżności szeregu potęgowego:

Zadania przykładowe

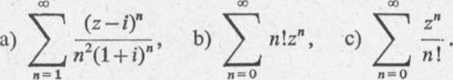
Rozwiązanie, a) Mamy

(z-O"

(1)

n²(l + i)ⁿ"