108310

Zadanie 4

Posługując się funkcją użyteczności Dixita-Stiglitza, oblicz poziom użyteczności w każdym z przypadków przedstawionych w poniższej tabeli.

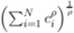
, gdzie Cj jest wielkością konsumpcji /-tej odmiany.

U =

	P = 1	r- o II o.	II c	p = 0.25	(> = 0.1
Cl = 3 C2 = 0 C3 = 0
C| = 1 C-2 = 1 c3 = 1

Jakie wnioski płyną z tej tabeli, co do potencjalnych źródeł korzyści z handlu? Jaką rolę w tej analizie odgrywa parametr p?

Zadanie 5/

Rozważamy uproszczony model Dixita-Stiglitza (Marrewijk, rozdz. 10). Załóżmy, że użyteczność reprezentatywnego konsumenta dana jest przez:

gdzie /> € (0.1) jest parametrem zamiłowania do różnorodności (love-for-varieły). Kraj dysponuje zasobem L jednostek pracy (jedyny czynnik produkcji). Wynagrodzenia oznaczmy przez w. Załóżmy dalej, że na rynku krajowym istnieje N firm, które produkują dobra będące niedoskonałymi substytutami. Firmy konkurują w ramach modelu konkurencji monopolistycznej. Każda firma ma pewną siłę monopolistyczną i ustalając cenę swojego produktu bierze ceny konkurentów za dane oraz traktuje wpływ swojej własnej ceny na ogólny rynkowy poziom cen jako zaniedbywalny. Wszystkie firmy mają dostęp do takiej samej technologii. Funkcja kosztu jest dana następująco:

/. = / + mx„

gdzie /, to ilość jednostek pracy potrzebna do wytworzenia x, jednostek produktu, / to stały nakład pracy zaś m to krańcowy nakład pracy. W gospodarce występuje pełne zatrudnienie, czyli L = A^r/j.

(a) Zapisz problem maksymalizacji użyteczności konsumenta. Wyprowadź funkcje popytu na poszczególne odmiany dobra. Dla uproszczenia zapisów przyjmijmy, że rynkowy indeks

2