118379

FV = PV(\ + r)'

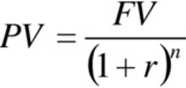
Strumienie płatności (dla \vplat dokonywanych z dołu)

Wartość przyszła:

FV = R_x(l + r)"'¹ + R₂(l + r)" ² +... + R,, =X^/?;(l ⁺

7=1

dla Z?, =/?-,= /?

r

Wartość bieżąca:

PV = R,

+ R,

(1 + r)^{1    2}(l ₊ r)²

"0 + r)

-=Yr

n J

7=1

(i+^y

dla = R₂ = R

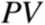
r(1 + r)

gdzie:

- wartość annuitetowa (wielkości o tej samej wartości występujące w stałych odstępach czasu)

Renta wieczysta (z dołu) (/?„.):

R_w = Pxr

Kapitalizacja ciągła