118457

4.    Sprawdź czy funkcja />, = /(/) = -—— dla i = 1,2,3,... jest rozkładem

j i + l

prawdopodobieństwa zmiennej losowej / Oblicz prawdopodobieństwo /’(/ s 3).

Odp.: TAK

P(l* 3) = i

5.    Dana jest zmienna losowa o rozkładzie geometrycznym p_k = P(X = k)= pq^k'^x dla

k = 1,2,... gdzie 0 < /? < 1 p + q = \. Sprawdź czy spełniony jest warunek unormowania. Oblicz: wartość oczekiwaną, wariancję, funkcję tworzącą momenty, funkcję charakterystyczną oraz funkcję tworzącą.

Odp: EX =—, D~X = —^, M(t)= Ee* = Ą-qćY, <p(t)= Ee^M = p\\-qe“Y,

P    P‘

s(z)=Yp^=T^£L-

»    1 ~qz

Wskazówka skorzystaj ze wzom na sumę wyrazów nieskończonego ciągu geometrycznego

6.

Zmienna losowa X ma rozkład Poissona: P(X = k) =

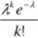
dla k =0,1,2. ..

A > 0.

Sprawdź wanutek unormowania. Wyznacz wartość oczekiwaną i wariancję zmiennej losowej X . Wyznacz funkcję tworzącą momenty, funkcję charakterystyczną, funkcję tworzącą.

Odp: EX = A, EX^l = A, M(l) = e^''\    =    s(z)= e'^,('"^l)

Wskazówka: V-— = e¹

h k\

7. Linia automatyczna przy normalnym ustawieniu może wypuścić przedmiot wykonany wadliwie z praw dopodobieństwem p Znaleźć średnią ilość przedmiotów' wypuszczonych pomiędzy dwoma wadliwymi przedmiotami

Odp.: EX = —

P

8 Z partii 250 sztuk towaru, zawierającej 18 szńtk wadliwych wylosowano bez zwrotu próbę 10 elementową W procesie kontroli wyrywkowej partia zostanie odrzucona, gdy w próbce znajdzie się 2 lub więcej sztuk wadliwych. Oblicz prawdopodobieństwo przyjęcia dartej partii towaru.

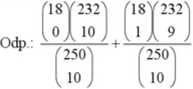
9 Próba może być pomyślna z prawdopodobieństwem p lub niepomyślna z

prawdopodobieństwem 1 - p. Prawdopodobieństwo warunkowe Hm) osiągnięcia celu po