123279

Definicja operatora

Rozważmy przestrzeń liniową, będącą zbiorem ciągłych funkcji zespolonych, określonych w pewnym przedziale domkniętym [a,b] liczb rzeczywistych.

W notacji Diraca, funkcje jako elementy przestrzeni zapisujemy w postaci:

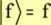
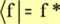
W przestrzeni tej występują działania (muszą spełniać szereg warunków, np. muszą być przemienne oraz mieć elementy zerowe):

-    dodawanie funkcji

-    mnożenie funkcji przez liczbę zespoloną.

Przestrzeń jest unitarna, jeżeli dodatkowo jest zdefiniowane mnożenie skalarne

funkcji, które będziemy zapisywać w postaci:    Tzw. norma

b

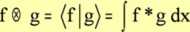
a

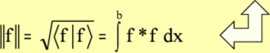
a

Operator-odwzorowanie, przekształcające dowolną funkcję należącą do jakiejś przestrzeni w innąfunkcję, należącą do tej samej przestrzeni

Af = g