49657
POCHODNA
Pochodna
Granica z ilorazu różnicowego przy dążącym do zera.
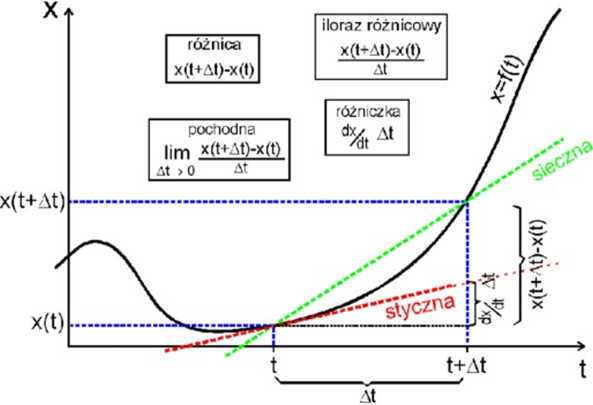
Przykład pochodnej: szybkość v, która jest pochodną położenia (współrzędnej .x) względem czasu Uwaga: Iloraz różnicowy NIE JEST tangensem nachylenia siecznej!
Jest natomiast współczynnikian kierunkowym siecznej.
Pochodna NIE JEST tangensem kąta nachylenia stycznej!
Jest natomiast współczynnikiem kierunkowym stycznej.
Tangens kąta nachylenia prostej jest współczynnikiem nachylenia tylko wówczas, gdy osie dotyczą tych samych wielkości fizycznych (np. jednostki miary) i są wykreślone w tej samej skali.
Wyszukiwarka
Podobne podstrony:
41605 Zdjęcie0091 kinematyka. ~~ciała sztywnego Obliczając granicę ilorazu różnicowego przy t dążący
76608 Zdjęcie0091 (12) KINEMATYKA.ciała sztywnego Obliczając granicę ilorazu różnicowego przv t dążą
Granicę właściwą ilorazu różnicowego przy Ax-»0 nazywamy pochodną funkcji f w punkcie x0 i oznaczamy
46 I. Teoria granic 29. Lematy o ciągach zbieżnych do zera. W dalszych twierdzeniach będziemy rozważ
MATEMATYKA095 182 ID. Rachunek różniczkowy pochodnej (można sprawdzić, że f (x)-»+oc przy x->l, s
ZADANIA STR 44 Ćwiczenia 4 Oblicznic ilorazu różnicowego. Obliczanie pochodnych funkcji na podstawie
164 III. Pochodne i różniczki przy tym wskaźnik x nie jest związany z tą szczególną wartością x0
zadania 2 Pokazać, żc funkcja f(z) = z2. z £ C, ma pochodną zespoloną tylko w z = 0. Pokazać, żc ilo
174 III. Pochodne i różniczki Jeśli Ax dąży do zera, to i Au też dąży do zera [96, 2°], a wtedy, jak
174 III. Pochodne i różniczki Jeśli Ax dąży do zera, to i Au też dąży do zera [96, 2°], a wtedy, jak
4. POCHODNE FUNKCJI4.1 PODSTAWOWE POJĘCIA Def.4.1.1 (iloraz różnicowy) Niech funkcja f będzie określ
174 III. Pochodne i różniczki Jeśli Ax dąży do zera, to i Au też dąży do zera [96, 2°], a wtedy, jak
więcej podobnych podstron