49695

V- -Jvf- 2v^sin« + gY

Teraz obliczamy położenie ciała

x = Vo,/

czyli

x = v₀ cos 61

czyli

y - vp,/^(l/2)rt_>r y = v₀ sinO t - (Itygfi

Długość wektora położenia r można teraz obliczyć dla dowolnej chwili / z zależności

r = -Jx² + y²

Sprawdźmy po jakim torze ponisza się nasz obiekt tzn. znajdźmy równanie krzywej y(x).

Mamy równania x(/) i y(t). Równanie v(.t) obliczymy eliminując t z równali (3.2) i (3.3). Z równania (3.2)

/ = .r/v_ocos0

więc równanie (3.3) przyjmuje postać

>-= (tg0 ).r -

2(v₀cos ey

Otrzymaliśmy rówiianie paraboli (ramionami w dól).

Z równania paraboli obliczamy zasięg Z czyli znajdziemy miejsca zerowe. Do równania (3.3) wstawiamy x = Z oraz y = 0 i otrzymujemy po przekształceniach dwa miejsca zerowe

Z = 0

oraz

„ 2vł sin0 cosd vl . «,_n Z • —    - ■ — sm2fi

g    g

Z równania (3.4) wynika, że zasięg jest maksymalny gdy 0= 45°

Zauważmy, że omawiany ruch odbywa się po linii krzywej.

W poprzednich wykładach mówiliśmy o przyspieszeniu zmieniającym wartość prędkości, a nie jej kierunek (zwrot). Mówiliśmy o przy spieszeniu sty cznym.

Rozpatrzmy teraz sytuacje gdy wartość prędkości się nie zmienia a zmienia się kierunek.

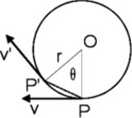
Ruch jednostajny po okręgu

Rozważmy zamieszczony obok rysunek. Punkt P - położenie punktu materialnego w chwili /, a P' - położenie w chwili t + At. Wektory v, v* mają jednakowe długości ale różnią się kierunkiem; są styczne do toru (krzywej) odpowiednio w punktach P i P'.