49840

d.    napisać równania równowagi.

e.    rozwiązać układ równań zestawiony w poprzednim punkcie i wyznaczyć wielkości niewiadome.

ZADANIA

Przykład 1

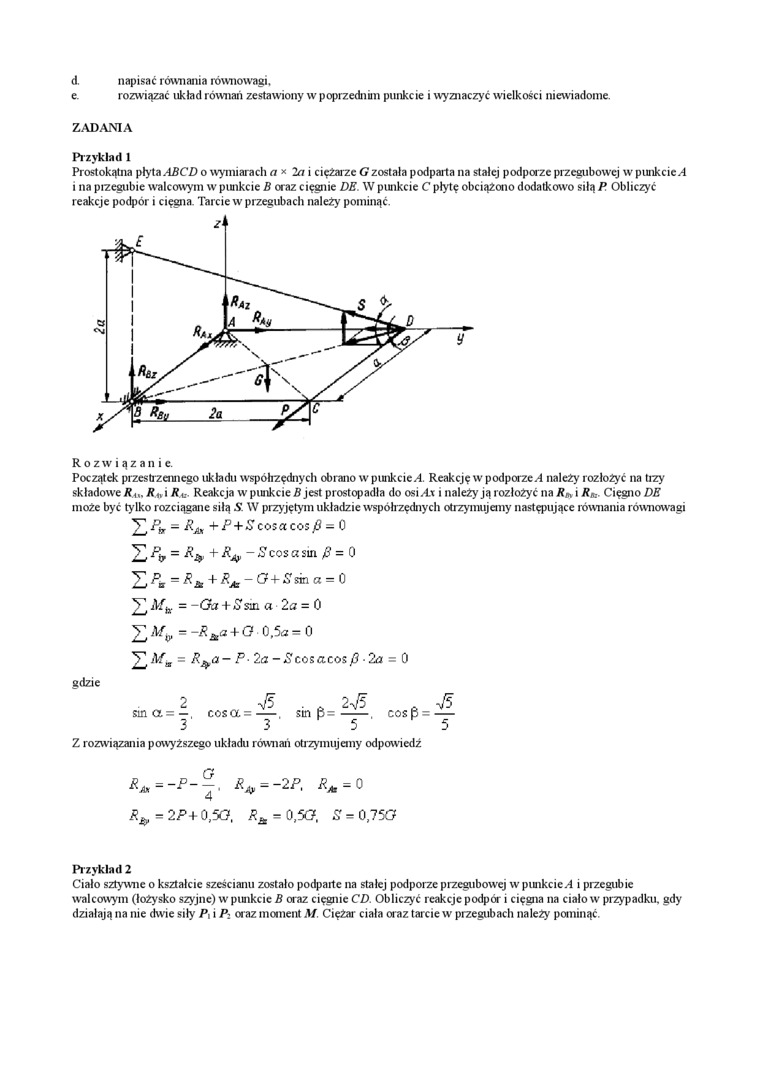
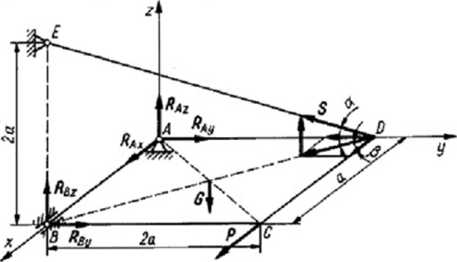
Prostokątna płyta ABCD o wymiarach a * 2a i ciężarze Gzostała podparta na stałej podporze przegubowej w punkcie.-1 i na pizegubie walcowym w punkcie B oraz cięgnie DE. W punkcie C płytę obciążono dodatkowo siłą P Obliczyć reakcje podpór i cięgna. Tarcie w przegubach należy pominąć.

Rozwiązanie.

Początek przestrzennego układu wspóhzędnych obrano w pimkcie/t. Reakcję w podporze A należy rozłożyć na tizy składowe R_t„ R_Ąi i /?.*. Reakcja w punkcie Sjest prostopadła do osi At i należy ją rozłożyć na Ri R^. Cięgno DE może być tylko rozciągane siłą S. W przyjętym układzie współrzędny cli otrzymujemy następujące równania równowagi ^/fr. -    + P+Scosacos fi = 0

^ Pę = Rfy + Rjy - £cos a sin fi = 0 = ^R* ^+RAz - O+Sski a = 0 2 M_h. = - Ga + Ssn a 2a = 0 ^^=-^ + 0 0,53=0 V Af_k = Rj^a- P■ 2a -Scosacos fi -2a = 0

gdzie

2    3 ■ * 23    ^3

sina=—, cos a =—. sin p=-. cos 6 = —

3    3    5    5

Z rozwiązania powyższego układu równań otrzymujemy odpowiedź

R« = -P-°. R_tf=-2P, R_M = 0

Rą, =2P+ 0,50, ** = 0,5(7. £ = 0,75O

Przykład 2

Ciało sztywne o kształcie sześcianu zostało podparte na stałej podporze przegubowej w punkcie A i przegubie walcowym (łożysko szyjne) w punkcie B oraz cięgnie CD. Obliczyć reakcje podpór i cięgna na ciało w przypadku, gdy działają na nie dwie siły P, i P_: oraz moment M. Ciężar ciała oraz tarcie w przegubach należy pominąć.