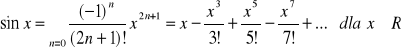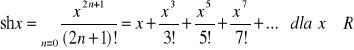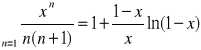1. CAŁKI NIEWŁAŚCIWE

1.1 CAŁKI NIEWŁAŚCIWE PIERWSZEGO RODZAJU

Def. 1.1.1 (całka niewłaściwa na półprostej)

Niech funkcja
będzie całkowalna na przedziałach [a,T] dla każdego T>a. Całkę niewłaściwą pierwszego rodzaju funkcji f na przedziale [a,∞) definiujemy wzorem:

.

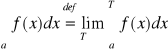
Jeżeli granica po prawej stronie znaku równości jest skończona, to mówimy, że całka niewłaściwa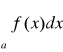
jest zbieżna. Jeżeli granica ta jest równa ∞ lub -∞, to mówimy, że całka jest rozbieżna odpowiednio do ∞ lub -∞. W pozostałych przypadkach mówimy, że całka jest rozbieżna.

Analogicznie definiuje się całkę niewłaściwą pierwszego rodzaju na przedziale (-∞,b]:

.

Def. 1.1.2 (całka niewłaściwa na prostej)

Niech funkcja
będzie całkowalna na przedziałach [S,T] dla dowolnych S i T takich, że -∞ < S < T < ∞. Całkę niewłaściwą pierwszego rodzaju funkcji f na przedziale (-∞,∞) definiujemy wzorem:

,

gdzie a oznacza dowolną liczbę rzeczywistą. Jeżeli obie całki po prawej stronie znaku równości są zbieżne, to mówimy, że całka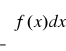
jest zbieżna. Jeżeli jedna z tych całek jest rozbieżna do -∞ lub ∞, a druga jest zbieżna albo rozbieżna odpowiednio do -∞ lub ∞, to mówimy, że całka jest rozbieżna do -∞ lub ∞. W pozostałych przypadkach mówimy, że całka ta jest rozbieżna.

Uwaga. Jeżeli całki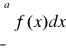
,
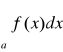
są zbieżne dla pewnego a∈R, to są zbieżne dla każdego a∈R i ich suma nie zależy od a.

Fakt 1.1.3 (zbieżność całek postaci
)

Niech a>0. Wtedy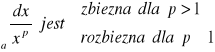
.

Uwaga. Analogiczny fakt jest prawdziwy także dla całek
, gdzie b<0, o ile funkcja podcałkowa jest poprawnie określona.

1.2 KRYTERIA ZBIEŻNOŚCI CAŁEK NIEWŁAŚCIWYCH PIERWSZEGO RODZAJU

Tw. 1.2.1 (kryterium porównawcze)

Jeżeli

1. 0 ≤ f(x) ≤ g(x) dla każdego x ∈ [a,∞),

2. funkcje f i g są całkowalne na przedziałach [a,T] dla T>a,

3. całka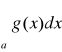
jest zbieżna

to całka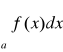
jest zbieżna.

Uwaga. Twierdzenie powyższe pozostanie prawdziwe, gdy nierówności w założeniu 1 są prawdziwe dla każdego x ∈[a^*,∞), gdzie a^*>a. Jeżeli założenie 3 tego twierdzenia ma postać „całka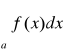
jest rozbieżna”, to w tezie otrzymamy „całka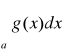
jest rozbieżna”. Prawdziwe jest także analogiczne kryterium porównawcze dla całek niewłaściwych postaci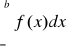
.

Tw. 1.2.2 (kryterium ilorazowe)

Niech funkcje dodatnie f i g będą całkowalne na przedziałach [a,T] dla każdego T>a oraz niech
, gdzie 0<k<∞. Wówczas

całka
jest zbieżna ⇔ całka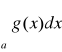
jest zbieżna.

Uwaga. Prawdziwe jest także analogiczne kryterium ilorazowe dla całek niewłaściwych postaci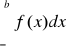
.

1.3 ZBIENOŚĆ BEZWZGLĘDNA CAŁEK NIEWŁAŚCIWYCH PIERWSZEGO RODZAJU

Def. 1.3.1 (zbieżność bezwzględna całek niewłaściwych pierwszego rodzaju)

Niech funkcja f będzie całkowalna na przedziałach [a,T] dla każdego T>a. Całka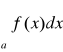
jest zbieżna bezwzględnie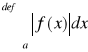
jest zbieżna.

Podobnie określa się zbieżność bezwzględną całek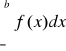
,
.

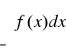
Tw. 1.3.2 (o zbieżności całek niewłaściwych zbieżnych bezwzględnie)

Niech funkcja f będzie całkowalna na przedziałach [a,T] dla każdego T>a. Jeżeli całka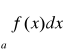
jest zbieżna bezwzględnie, to całka
jest zbieżna. Ponadto

.

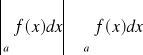
Uwaga. Powyższe twierdzenie jest prawdziwe także dla pozostałych rodzajów całek niewłaściwych pierwszego rodzaju. Twierdzenie odwrotne nie jest prawdziwe dla dowolnej funkcji, np. całka niewłaściwa z funkcji
na przedziale [1,∞) jest zbieżna, ale nie jest zbieżna bezwzględnie.

1.4 CAŁKI NIEWŁAŚCIWE DRUGIEGO RODZAJU

Def. 1.4.1 (całki niewłaściwe drugiego rodzaju)

Niech funkcja
będzie nieograniczona na prawostronnym sąsiedztwie punktu a oraz całkowalna na przedziałach [a+ε,b] dla każdego 0 < ε < b - a. Całkę niewłaściwą drugiego rodzaju funkcji f na przedziale (a,b] definiujemy wzorem:

.

Jeżeli granica po prawej stronie znaku równości jest skończona, to mówimy, że całka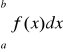
jest zbieżna. Jeżeli granica ta jest równa ∞ lub -∞, to mówimy, że całka jest rozbieżna odpowiednio do ∞ lub -∞. W pozostałych przypadkach mówimy, że całka ta jest rozbieżna.

Analogicznie definiuje się całkę niewłaściwą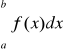
funkcji f nieograniczonej na lewostronnym sąsiedztwie punktu b:

.

Jeżeli funkcja f jest określona i ograniczona na przedziale (a,b] oraz całkowalna na przedziałach [a+ε,b] dla każdego 0 < ε < b - a, to całka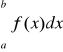
obliczona według powyższej definicji jest zbieżna. Podobnie jest da funkcji określonej na przedziale [a,b).

Fakt 1.4.2 (o zbieżności całek
)

Niech b>0. Wtedy całka niewłaściwa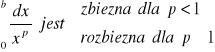
.

Analogiczny fakt jest prawdziwy także dla całek
, gdzie a<0, o ile funkcja podcałkowa jest poprawnie określona.

Def. 1.4.3 (całki niewłaściwe drugiego rodzaju, ciąg dalszy)

Niech funkcja
, gdzie c∈(a,b), będzie nieograniczona na obustronnych sąsiedztwach punktu c oraz całkowalna na przedziałach [a,c-ε ], [c+ε,b] dla każdego 0 < ε < min{b - c, c - a}. Całkę niewłaściwą drugiego rodzaju funkcji f na przedziale [a,b] definiujemy wzorem:

.

Jeżeli obie całki po prawej stronie znaku równości są zbieżne, to mówimy, że całka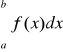
jest zbieżna. Jeżeli jedna z tych całek jest rozbieżna do -∞ lub ∞, a druga jest zbieżna albo rozbieżna odpowiednio do -∞ lub ∞, to mówimy, że całka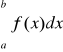
jest rozbieżna do -∞ lub ∞. W pozostałych przypadkach mówimy, że całka ta jest rozbieżna.

W podobny sposób określa się całki niewłaściwe z funkcji nieograniczonych na sąsiedztwach punktów c₁, c₂, ..., c_n ∈ [a,b]. Na przykład dla funkcji
, nieograniczonej na prawostronnym sąsiedztwie punktu a i na lewostronnym sąsiedztwie punktu b oraz całkowalnej na przedziałach [a + ε, b - ε] dla każdego
, przyjmujemy:

,

gdzie d jest dowolnym punktem przedziału (a,b).

1.5 KRYTERIA ZBIEŻNOŚCI CAŁEK NIEWŁAŚCIWYCH DRUGIEGO RODZAJU

Tw. 1.2.1 (kryterium porównawcze)

Jeżeli

1. 0 ≤ f(x) ≤ g(x) dla każdego x ∈ (a,b],

2. funkcje f i g są całkowalne na [a+ε,b] dla 0 < ε < b - a,

3. całka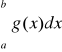
jest zbieżna

to całka
jest zbieżna.

Uwaga. Twierdzenie powyższe pozostanie prawdziwe, gdy nierówności w założeniu 1 są prawdziwe dla każdego x ∈ (a,b^*], gdzie a<b^*<b. Jeżeli założenie 3 tego twierdzenia ma postać „całka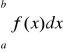
jest rozbieżna”, to w tezie otrzymamy „całka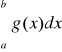
jest rozbieżna”. Prawdziwe jest także analogiczne kryterium porównawcze dla funkcji określonych na przedziale [a,b) i nieograniczonych na lewostronnym sąsiedztwie punktu b.

Tw. 1.2.2 (kryterium ilorazowe)

Niech funkcje dodatnie f i g będą całkowalne na przedziałach [a+ε,b] dla każdego 0 < ε < b - a oraz niech
, gdzie 0<k<∞. Wówczas

całka
jest zbieżna ⇔ całka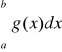
jest zbieżna.

Uwaga. Prawdziwe jest także analogiczne kryterium dla całek niewłaściwych na przedziale [a,b).

2. SZEREGI LICZBOWE I POTĘGOWE

2.1 DEFINICJE I PODSTAWOWE TWIERDZENIA

Def. 2.1.1 (szereg, suma częściowa szeregu)

Niech (a_n) będzie ciągiem liczbowym. Szeregiem liczbowym nazywamy ciąg (S_n), gdzie S_n = a₁ + a₂ + … + a_n. Szereg taki oznaczamy przez
. Liczbę a_n nazywamy n-tym wyrazem, a liczbę S_n n-tą sumą częściową tego szeregu.

Def. 2.1.2 (szereg zbieżny i rozbieżny, suma szeregu)

Mówimy, że szereg
jest zbieżny, jeżeli istnieje skończona granica ciągu (S_n). Jeżeli
albo
, to mówimy, że szereg
jest rozbieżny odpowiednio do -∞ albo do ∞. W pozostałych przypadkach mówimy, że szereg jest rozbieżny. Sumą szeregu zbieżnego nazywamy granicę
i oznaczamy ją tym samym symbolem co szereg.

Uwaga. Analogicznie można zdefiniować szereg
, gdzie n₀ ∈ Z oraz jego sumę.

Fakt 2.1.3 (zbieżność szeregu geometrycznego)

Szereg geometryczny
jest zbieżny wtedy i tylko wtedy, gdy
. Dla zbieżnego szeregu geometrycznego mamy:

.

Uwaga. Przyjmujemy tutaj, że
.

Tw. 2.1.4 (warunek konieczny zbieżności szeregu)

Jeżeli szereg
jest zbieżny, to
.

Uwaga. Twierdzenie odwrotne nie jest prawdziwe. Świadczy o tym przykład ciągu
. Mamy bowiem
, ale szereg
jest rozbieżny do ∞. Powyższe twierdzenie zapisane w równoważnej postaci: jeżeli
albo granica
nie istniej, to szereg
jest rozbieżny, stosujemy do uzasadniania rozbieżności niektórych szeregów.

2.2 KRYTERIA ZBIEŻNOŚCI SZEREGÓW

Tw. 2.2.1 (kryterium całkowe)

Niech funkcja
gdzie n₀∈N, będzie nierosnąca. Wówczas

szereg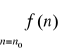
jest zbieżny ⇔ całka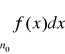
jest zbieżna.

Uwaga. Reszta tego szeregu, to jest wyrażenie
, spełnia oszacowanie:

.

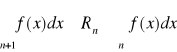
Fakt 2.2.2 (zbieżność szeregów postaci
)

Szereg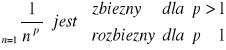
.

Tw. 2.2.3 (Kryterium porównawcze)

1. 0 ≤ an ≤ bn dla każdego n ≥ n0 2. szereg jest zbieżny

⇒ szereg jest zbieżny.

Uwaga. Jeżeli założenie 2 ma postać „szereg
jest rozbieżny”, to w tezie otrzymamy: „szereg
jest rozbieżny”.

Tw. 2.2.4 (kryterium ilorazowe)

Niech a_n, b_n > 0 dla każdego n ≥ n₀ oraz niech
, gdzie 0<k<∞. Wówczas

szereg
jest zbieżny ⇔ szereg
jest zbieżny.

Tw. 2.2.5 (Kryterium d'Alemberta)

1. Jeżeli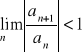
, to szereg
jest zbieżny.

2. Jeżeli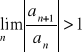
, to szereg
jest rozbieżny.

Uwaga. Jeżeli zamiast założenia podanego w punkcie 2 spełniony jest warunek
dla każdego n ≥ n₀, to szereg
jest nadal rozbieżny. Jeżeli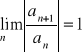
, to kryterium a'Alemberta nie rozstrzyga, czy szereg
jest zbieżny. Np. dla ciągów
,
mamy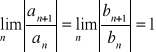
, ale szereg
jest zbieżny, natomiast szereg
jest rozbieżny.

Tw. 2.2.6 (Kryterium Cauchy'ego)

1. Jeżeli
, to szereg
jest zbieżny.

2. Jeżeli
, to szereg
jest rozbieżny.

Uwaga. Jeżeli
, to kryterium Cauchy'ego nie rozstrzyga, czy szereg
jest zbieżny.

2.3 ZBIEŻNOŚĆ BEZWZGLĘDNA SZEREGÓW

Tw. 2.3.1 (Leibniza o zbieżności szeregu naprzemiennego)

Jeżeli

1. ciąg (b_n) jest nierosnący od numeru n₀∈N,

2.

to szereg naprzemienny
jest zbieżny.

Ponadto prawdziwe jest następujące oszacowanie reszty szeregu:

dla każdego n ≥ n₀.

Def. 2.3.2 (zbieżność bezwzględna szeregu)

Szereg
jest zbieżny bezwzględnie
szereg
jest zbieżny.

Tw. 2.3.3 (o zbieżności szeregów zbieżnych bezwzględnie)

Jeżeli szereg liczbowy jest zbieżny bezwzględnie, to jest zbieżny.

Uwaga. Twierdzenie odwrotne nie jest prawdziwe. Świadczy o tym przykład szeregu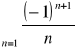
, który jest zbieżny, ale nie jest zbieżny bezwzględnie.

Def. 2.3.4 (szereg zbieżny warunkowo)

Szereg zbieżny, który nie jest zbieżny bezwzględnie, nazywamy szeregiem zbieżnym warunkowo.

Fakt 2.3.5 (sumy ważniejszych szeregów)

2.4. SZEREGI POTĘGOWE

Def. 2.4.1 (szereg potęgowy)

Szeregiem potęgowym o środku w punkcie x₀∈R nazywamy szereg postaci:

, gdzie x∈R oraz c_n∈R dla n=0, 1, 2, ....

Uwaga. W tym paragrafie przyjmujemy, że
. Liczby c_n nazywamy współczynnikami szeregu potęgowego.

Def. 2.4.2 (promień zbieżności szeregu potęgowego)

Promieniem zbieżności szeregu potęgowego
nazywamy liczbę R określoną równością:

,

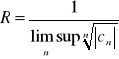
gdy
. Ponadto przyjmujemy R = 0, gdy
oraz R = ∞, gdy
.

Uwaga. Promień zbieżności szeregu potęgowego może być także obliczany ze wzoru:

albo ze wzoru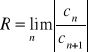
,

o ile te granice istnieją.

Tw. 2.4.3 (Cauchy'ego - Hadamarda)

Niech 0 < R < ∞ będzie promieniem zbieżności szeregu potęgowego
. Wtedy szereg ten jest:

a) zbieżny bezwzględnie w każdym punkcie przedziału (x₀ - R , x₀ + R),

b) rozbieżny w każdym punkcie zbioru (-∞ , x₀ - R )∪(x₀ + R, ∞).

Uwaga. W obu końcach przedziału (x₀ - R , x₀ + R) szereg potęgowy może być zbieżny lub rozbieżny. Gdy R = 0, to szereg potęgowy jest zbieżny jedynie w punkcie x₀. Gdy R = ∞, to szereg potęgowy jest zbieżny bezwzględnie na całej prostej.

Def. 2.4.4 (przedział zbieżności szeregu potęgowego)

Przedziałem zbieżności szeregu potęgowego
nazywamy zbiór:

.

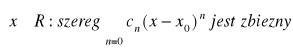
Tw. 2.4.5 (o rozwijaniu funkcji w szereg potęgowy)

Jeżeli:

1. funkcja f ma na przedziale (x₀ - δ, x₀ + δ) pochodne dowolnego rzędu,

2. dla każdego x∈(x₀ - δ, x₀ + δ) spełniony jest warunek
, gdzie

oznacza n-tą resztę we wzorze Taylora dla funkcji f na przedziale [x₀,x] lub [x,x₀], to

dla każdego
.

Uwaga. Zamiast założenia 2 powyższego twierdzenia można przyjąć, że:

dla każdego
oraz dla każdego
.

Szereg potęgowy występujący w tezie tego twierdzenia nazywamy szeregiem Taylora funkcji f w punkcie x₀. Gdy x₀ = 0, to szereg ten nazywamy szeregiem Maclaurina.

Tw. 2.4.6 (o jednoznaczności rozwinięcia funkcji w szereg potęgowy)

Jeżeli
dla każdego
, gdzie δ > 0, to

dla n = 0, 1, 2, ... .

Fakt 2.4.7 (szeregi Maclaurina niektórych funkcji elementarnych)

Tw. 2.4.8 (o różniczkowaniu szeregu potęgowego)

Niech 0 < R ≤ ∞ będzie promieniem zbieżności szeregu potęgowego
. Wtedy:

dla każdego
.

Uwaga. Na przedziale (-R,R) suma szeregu potęgowego ma ciągłe pochodne dowolnego rzędu. Podobny wzór jest prawdziwy także dla szeregu potęgowego postaci
:

Niech 0 < R ≤ ∞ będzie promieniem zbieżności szeregu potęgowego
. Wtedy:

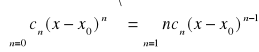
dla każdego
.

Tw. 2.4.9 (o całkowaniu szeregu potęgowego)

Niech 0 < R ≤ ∞ będzie promieniem zbieżności szeregu potęgowego
. Wtedy:

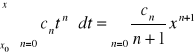
dla każdego
.

Uwaga. Podobny wzór jest prawdziwy także dla szeregu potęgowego postaci
:

Niech 0 < R ≤ ∞ będzie promieniem zbieżności szeregu potęgowego
. Wtedy:

dla każdego
.

Fakt 2.4.10 (sumy ważniejszych szeregów potęgowych)

Uwaga. Wszystkie podane wyżej wzory są prawdziwe dla każdego x∈(-1, 1).

3. FUNKCJE DWÓCH I TRZECH ZMIENNYCH

3.1 ZBIORY NA PŁASZCZYŹNIE I W PRZESTRZENI

Def. 3.1.1 (płaszczyzna, przestrzeń)

Przestrzenią dwuwymiarową (płaszczyzną) nazywamy zbiór wszystkich par uporządkowanych (x,y), gdzie x,y ∈ R. Przestrzeń dwuwymia­rową oznaczamy przez R²:

.

Podobnie, przestrzenią trójwymiarową (przestrzenią) nazywamy zbiór wszystkich uporządkowanych (x,y,z), gdzie x, y, z ∈ R. Przestrzeń trójwy­mia­rową oznaczamy przez R³:

.

Elementy (x,y) oraz (x,y,z) tych przestrzeni nazywamy odpowiednio punktami płaszczyzny lub przestrzeni. Liczby x, y oraz x, y, z nazywamy odpowiednio współrzędnymi kartezjańskimi punktów (x,y) oraz (x,y,z).

Def. 3.1.2 (odległość punktów)

Odległość punktów P₁, P₂ płaszczyzny lub przestrzeni oznaczamy symbolem |P₁P₂| i określamy wzorem:

,

gdzie P₁ = (x₁,y₁), P₂ = (x₂,y₂) ∈ R² lub wzorem

,

gdzie P₁ = (x₁,y₁,z₁), P₂ = (x₂,y₂,z₂) ∈ R³.

Rys. 3.1.1 Odległość dwóch punktów na płaszczyźnie		Rys. 3.1.2 Odległość dwóch punktów w przestrzeni

Def. 3.1.3 (otoczenie punktu)

Otoczeniem o promieniu r > 0 punktu P₀ na płaszczyźnie lub przestrzeni nazywamy zbiór:

.

Otoczeniem punktu na płaszczyźnie jest koło otwarte o środku w danym punkcie. Otoczeniem punktu w przestrzeni jest kula otwarta o środku w danym punkcie.

Def. 3.1.4 (sąsiedztwo punktu)

Sąsiedztwem o promieniu r > 0 punktu P₀ na płaszczyźnie lub przestrzeni nazywamy zbiór:

.

Sąsiedztwem punktu na płaszczyźnie jest koło otwarte bez środka. Podobnie, sąsiedztwem punktu w przestrzeni jest kula otwarta bez środka.

Rys. 3.1.3 Otoczenie o promieniu r punktu P0 na płaszczyźnie	Rys. 3.1.4 Sąsiedztwo o promieniu r punktu P0 na płaszczyźnie

Def. 3.1.5 (zbiór ograniczony i nieograniczony)

Zbiór A jest ograniczony, jeżeli jest zawarty w otoczeniu pewnego punktu, tzn.

.

W przeciwnym przypadku mówimy, że zbiór A jest nieograniczony.

Rys. 3.1.5 Zbiór A jest ograniczony na płaszczyźnie

Def. 3.1.6 (punkt wewnętrzny zbioru, wnętrze zbioru)

Niech A będzie zbiorem na płaszczyźnie lub w przestrzeni. Punkt P jest punktem wewnętrznym zbioru A, jeżeli istnieje otoczenie tego punktu zawarte w zbiorze A, tzn.

.

Wnętrzem zbiór nazywamy zbiór wszystkich jego punktów wewnętrznych.

Def. 3.1.7 (punkt brzegowy zbioru, brzeg zbioru)

Niech A będzie zbiorem na płaszczyźnie lub w przestrzeni. Punkt P jest punktem brzegowym zbioru A, jeżeli w każdym otoczeniu tego punktu można znaleźć punkty należące do zbioru A i punkty nie należące do zbioru A, tzn.

.

Brzegiem zbioru nazywamy zbiór wszystkich jego punktów brzegowych.

Rys. 3.1.6 Punkt P jest punktem brzegowym zbioru A

Def. 3.1.8 (zbiór otwarty)

Zbiór jest otwarty, jeżeli każdy punkt tego zbioru jest jego punktem wewnętrznym.

Def. 3.1.9 (zbiór domknięty)

Zbiór jest domknięty, jeżeli zawiera swój brzeg.

Rys. 3.1.7 Zbiór A jest otwarty na płaszczyźnie		Rys. 3.1.8 Zbiór B jest domknięty w przestrzeni

Def. 3.1.10 (obszar, obszar domknięty)

Niepusty zbiór jest obszarem, jeżeli:

1. jest otwarty,

2. każde dwa punkty zbioru można połączyć łamaną całkowicie w nim zawartą.

Obszar łącznie ze swoim brzegiem nazywamy obszarem domkniętym.

Rys. 3.1.9 Zbiór A jest obszarem domkniętym na płaszczyźnie	Rys. 3.1.10 Zbiór B nie jest obszarem na płaszczyźnie

3.2 FUNKCJE DWÓCH I TRZECH ZMIENNYCH

Def. 3.2.1 (funkcja dwóch zmiennych)

Funkcją f dwóch zmiennych określoną na zbiorze A ⊂ R² o wartościach w R nazywamy przyporządkowanie każdemu punktowi ze zbioru A dokładnie jednej liczby rzeczywistej. Wartość funkcji f w punkcie (x,y) oznaczany przez f(x,y). Funkcję taką oznaczmy przez
lub
, gdzie (x,y) ∈ A.

Rys. 3.2.1 Ilustracja do definicji funkcji dwóch zmiennych

Def. 3.2.2 (funkcja trzech zmiennych)

Funkcją f trzech zmiennych określoną na zbiorze A ⊂ R³ o wartościach w R nazywamy przyporządkowanie każdemu punktowi ze zbioru A dokładnie jednej liczby rzeczywistej. Wartość funkcji f w punkcie (x,y,z) oznaczany przez f(x,y,z). Funkcję taką oznaczmy przez
lub
, gdzie (x,y,z) ∈ A.

Rys. 3.2.2 Ilustracja do definicji funkcji trzech zmiennych

Def. 3.2.3 (dziedzina, dziedzina naturalna)

Niech
, gdzie A jest podzbiorem płaszczyzny lub przestrzeni. Zbiór A nazywamy dziedziną funkcji f i oznaczamy przez D_f. Jeżeli dany jest tylko wzór określający funkcję, to zbiór tych punktów płaszczyzny (przestrzeni), dla których wzór ten ma sens, nazywamy dziedziną naturalną funkcji.

Def. 3.2.4 (wykres i poziomica funkcji dwóch zmiennych)

Wykresem funkcji f dwóch zmiennych nazywamy zbiór:

.

Poziomicą wykresu funkcji f, odpowiadającą poziomowi h∈R, nazywamy zbiór:

.

Rys. 3.2.3 Poziomica wykresu funkcji f odpowiadająca poziomowi h

Fakt 3.2.5 (wykresy ważniejszych funkcji dwóch zmiennych)

1. Wykresem funkcji

jest płaszczyzna o wektorze normalnym
przechodząca przez punkt (0,0,C).

2. Wykresem funkcji

jest paraboloida obrotowa, tj. powierzchnia powstała z obrotu paraboli z = ax² wokół osi Oz.

3. Wykresem funkcji

jest stożek, tj. powierzchnia powstała z obrotu półprostej z = kx dla x ≥ 0 wokół osi Oz.

4. Wykresem funkcji

jest górna (+) lub dolna (-) półsfera o środku w początku układu współrzędnych i promieniu R.

5. Wykresem funkcji

jest „siodło”.

Fakt 3.2.6 (przesunięcia i odbicia wykresów funkcji)

1. Wykres funkcji

powstaje z wykresu funkcji
przez przesunięcie o wektor
.

2. Wykres funkcji

powstaje z wykresu funkcji
przez symetrię względem płaszczyzny xOy.

Rys. 3.2.4 Przesunięcie wykresu funkcji o wektor		Rys. 3.2.5 Odbicie wykresu funkcji względem płaszczyzny xOy

Def. 3.2.7 (funkcja ograniczona)

Funkcja f dwóch zmiennych jest ograniczona na zbiorze
, jeżeli zbiór wartości funkcji f na zbiorze A jest ograniczony, tzn.

.

Uwaga. Definicja funkcji ograniczonej trzech zmiennych jest analogiczna. Definicje funkcji dwóch i trzech zmiennych ograniczonych z dołu lub z góry są podobne do odpowiednich definicji dla funkcji jednej zmiennej.

3.3 GRANICE FUNKCJI W PUNKCIE

Def. 3.3.1 (ciąg na płaszczyźnie)

Ciągiem punktów na płaszczyźnie nazywamy odwzorowanie zbioru liczb naturalnych w zbiór R². Wartość tego odwzorowania dla liczby naturalnej n nazywamy n-tym wyrazem ciągu i oznaczamy przez
. Ciąg taki oznaczamy przez
lub
. Zbiór wyrazów tego ciągu, tj. zbiór
, oznaczamy krótko przez
lub
.

Def. 3.3.2 (granica właściwa ciągu)

Ciąg (P_n) = ((x_n,y_n)) jest zbieżny do punktu P₀ = (x₀,y₀), co notujemy

lub
,

wtedy i tylko wtedy, gdy

oraz
.

Uwaga. Ciąg (P_n) jest zbieżny do punktu P₀, jeżeli w dowolnym otoczeniu punktu P₀ znajdują się prawie wszystkie wyrazy tego ciągu. Definicja ciągu punktów w przestrzeni i definicja granicy takiego ciągu są analogiczne do podanych powyżej.

Def. 3.3.3 (Heinego granicy właściwej funkcji w punkcie)

Niech f dwóch zmiennych będzie określona na zbiorze otwartym D z wyjątkiem być może punktu (x₀, y₀)∈D. Liczba g jest granicą właściwą funkcji f w punkcie (x₀,y₀), co zapisujemy

,

wtedy i tylko wtedy, gdy

.

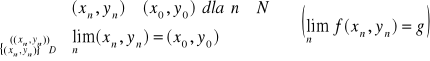
Uwaga. W podobny sposób można określić granicę funkcji w punkcie dowolnego zbioru na płaszczyźnie oraz granicę funkcji trzech zmiennych. Granicę funkcji f w punkcie (x₀,y₀) oznaczamy przez
. Można również pisać
, gdy
.

Def. 3.3.4 (Heinego granicy niewłaściwej funkcji w punkcie)

Niech f dwóch zmiennych będzie określona na zbiorze otwartym D z wyjątkiem być może punktu (x₀, y₀)∈D. Funkcja f ma w punkcie (x₀,y₀) granicę niewłaściwą ∞, co zapisujemy

,

wtedy i tylko wtedy, gdy

.

Uwaga. Definicja Heinego granicy niewłaściwej -∞ funkcji w punkcie jest analogiczna do definicji napisanej powyżej. Podobnie definiujemy obie granice niewłaściwe dla funkcji trzech zmiennych.

Tw. 3.3.5 (o granicy sumy)

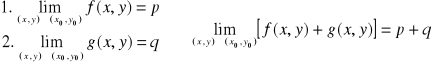
Tw. 3.3.6 (o granicy iloczynu)

Tw. 3.3.7 (o granicy ilorazu)

1. 2. dla każdego 3.

Uwaga. Ostatnie trzy twierdzenia są prawdziwe dla funkcji trzech zmiennych. W tych twierdzeniach dopuszczalne są także granice niewłaściwe, o ile odpowiednie działania z takimi symbolami są oznaczone. Do znajdowania granic funkcji dwóch i trzech zmiennych można stosować twierdzenia o dwóch i o trzech funkcjach, analogiczne do takich twierdzeń dla funkcji jednej zmiennej.

3.4 FUNKCJE CIĄGŁE

Def. 3.4.1 (funkcja dwóch zmiennych ciągła w punkcie)

Niech funkcja f będzie określona na zbiorze otwartym zawierającym punkt (x₀, y₀). Funkcja f jest ciągła w punkcie (x₀, y₀) wtedy i tylko wtedy, gdy

.

Def. 3.4.2 (funkcja dwóch zmiennych ciągła na zbiorze otwartym)

Funkcja jest ciągła na zbiorze otwartym D ⊂ R², jeżeli jest ciągła w każdym punkcie tego zbioru.

Uwaga. W podobny sposób można zdefiniować ciągłość funkcji w punkcie (x₀,y₀) dowolnego zbioru A ⊂ R² oraz ciągłość na tym zbiorze. Definicje ciągłości w punkcie i na zbiorach dla funkcji trzech zmiennych są analogiczne do podanych powyżej.

Tw. 3.4.3 (działania na funkcjach ciągłych)

Suma, iloczyn, iloraz oraz złożenie funkcji ciągłych są funkcjami ciągłymi.

Tw. 3.4.4 (Weierstrassa o osiąganiu kresów)

Jeżeli

1. zbiór D ⊂ R² jest domknięty i ograniczony,

2. funkcja f jest ciągła na D,

to

oraz

.

4. RACHUNEK RÓŻNICZKOWY FUNKCJI DWÓCH I TRZECH ZMIENNYCH

4.1 POCHODNE CZĄSTKOWE FUNKCJI

Def. 4.1.1 (pochodne cząstkowe pierwszego rzędu)

Niech funkcja f będzie określona na obszarze D ⊂ R² oraz niech (x₀,y₀) ∈ D. Pochodną cząstkową pierwszego rzędu funkcji f względem x w punkcie (x₀,y₀) określamy wzorem:

.

Pochodną tą oznaczamy także symbolami:
,
. Podobnie jest określona pochodna cząstkowa pierwszego rzędu funkcji f względem y w punkcie (x₀,y₀):

.

Pochodną tą oznaczamy także symbolami:
,
.

Uwaga. Analogicznie określa się pochodne cząstkowe pierwszego rzędu dla funkcji trzech zmiennych. Jeżeli granice określające pochodne cząstkowe są właściwe (niewłaściwe) ,to mówimy, że odpowiednie pochodne cząstkowe są właściwe (niewłaściwe).

Def. 4.1.2 (pochodne cząstkowe pierwszego rzędu na obszarze)

Jeżeli funkcja f ma pochodne cząstkowe pierwszego rzędu w każdym punkcie obszaru D ⊂ R², to funkcje
,
, gdzie
, nazywamy pochodnymi cząstkowymi pierwszego rzędu funkcji f na obszarze D i oznaczamy odpowiednio przez
,
lub f_x, f_y albo też D₁f, D₂f. Analogicznie określa się pochodne cząstkowe pierwszego rzędu na obszarze V ⊂ R³ dla funkcji trzech zmiennych.

Fakt 4.1.3 (interpretacja geometryczna pochodnych cząstkowych)

Niech funkcja z = f(x,y) ma pochodne cząstkowe pierwszego rzędu w punkcie (x₀,y₀). Ponadto niech α oznacza kąt nachylenia stycznej do krzywej otrzymanej w wyniku przekroju wykresu funkcji f płaszczyzną y = y₀ w punkcie (x₀,y₀,f(x₀,y₀)), do płaszczyzny xOy oraz niech β oznacza kąt nachylenia stycznej do krzywej otrzymanej w wyniku przekroju wykresu funkcji f płaszczyzną x = x₀. Wtedy

,
.

Rys 4.1.1 Interpretacja geometryczna po-chodnej cząstkowej		Rys 4.1.2 Interpretacja geometryczna po-chodnej cząstkowej

Pochodna cząstkowa
jest miarą lokalnej szybkości wzrostu funkcji f względem zmiennej x przy ustalonej wartości zmiennej y. Podobnie jest dla pochodnej cząstkowej
oraz dla pochodnych cząstkowych funkcji trzech zmiennych.

Uwaga. Odmiennie niż dla funkcji jednej zmiennej wygląda związek między ciągłością funkcji dwóch zmiennych a istnieniem pochodnych cząstkowych. Funkcja może mieć w punkcie obie pochodne cząstkowe, ale nie musi być w tym punkcie ciągła.

Def. 4.1.4 (pochodne cząstkowe drugiego rzędu)

Niech funkcja f ma pochodne cząstkowe
,
na obszarze D ⊂ R² oraz niech (x₀,y₀) ∈ D. Pochodne cząstkowe drugiego rzędu funkcji f w punkcie (x₀,y₀) określamy wzorami:

,

,

,

.

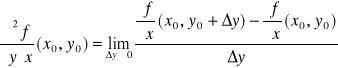
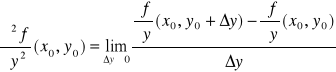
Powyższe pochodne oznaczamy także odpowiednio przez f_xx(x₀,y₀), f_xy(x₀,y₀), f_yx(x₀,y₀), f_yy(x₀,y₀) albo też D₁₁f(x₀,y₀), D₁₂f(x₀,y₀), D₂₁f(x₀,y₀), D₂₂f(x₀,y₀).

Uwaga. Analogicznie określa się pochodne cząstkowe drugiego rzędu funkcji trzech zmiennych.

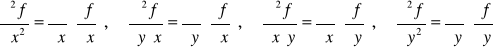
Def. 4.1.5 (pochodne cząstkowe drugiego rzędu na obszarze)

Jeżeli funkcja f ma pochodne cząstkowe drugiego rzędu w każdym punkcie obszaru D ⊂ R², to funkcje

,
,
,
,

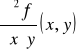
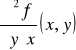
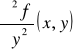
gdzie (x,y) ∈ D, nazywamy pochodnymi cząstkowymi drugiego rzędu funkcji f na obszarze D i oznaczamy odpowiednio przez
,
,
,
lub przez f_xx, f_xy, f_yx, f_yy albo też D₁₁f, D₁₂f, D₂₁f, D₂₂f.

Uwaga. Analogicznie określa się pochodne cząstkowe drugiego rzędu funkcji trzech zmiennych na obszarze V ⊂ R³.

Def. 4.1.6 (pochodne cząstkowe wyższych rzędów)

Niech funkcja f ma pochodne cząstkowe rzędu n ≥ 2 na otoczeniu punktu (x₀,y₀). Pochodne cząstkowe pierwszego rzędu w punkcie (x₀,y₀) pochodnych cząstkowych rzędu n funkcji f nazywamy pochodnymi cząstkowymi rzędu n + 1 funkcji f w punkcie (x₀,y₀). Jeżeli funkcja f ma pochodne cząstkowe rzędu n w każdym punkcie obszaru D, to mówimy, że na obszarze D są określone pochodne cząstkowe rzędu n funkcji f. Pochodną cząstkową n-tego rzędu funkcji f w punkcie (x₀,y₀), powstałą w wyniku k-krotnego różniczkowania względem zmiennej x i następnie l-krotnego różniczkowania względem zmiennej y, gdzie k + l = n, oznaczamy przez

.

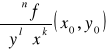
Analogicznie określa się i oznacza pochodne cząstkowe rzędu n ≥ 3 funkcji trzech zmiennych. Funkcja dwóch zmiennych ma 2ⁿ pochodnych cząstkowych rzędu n, a funkcje trzech zmiennych 3ⁿ pochodnych cząstkowych rzędu n. Pochodne cząstkowe, w których występuje różniczkowanie względem dwóch różnych zmiennych, nazywamy pochodnymi cząstkowymi mieszanymi.

Tw. 4.1.7 (Schwarza o pochodnych mieszanych)

Niech funkcja f będzie określona na otoczeniu punktu (x₀,y₀). Ponadto niech

1. pochodne cząstkowe
,
istnieją na otoczeniu punktu (x₀,y₀),

2. pochodne cząstkowe
,
będą ciągłe w punkcie (x₀,y₀).

Wtedy

.

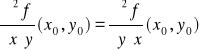
Uwaga. Prawdziwe są także analogiczne równości dla pochodnych mieszanych drugiego rzędu funkcji trzech zmiennych, a także dla pochodnych mieszanych wyższych rzędów.

4.2 RÓŻNICZKOWALNOŚĆ FUNKCJI

Def. 4.2.1 (funkcja różniczkowalna w punkcie)

Niech funkcja f będzie określona na otoczeniu punktu (x₀,y₀) oraz niech istnieją pochodne cząstkowe
,
. Funkcja f jest różniczkowalna w punkcie (x₀,y₀) wtedy i tylko wtedy, gdy spełniony jest warunek:

.

Uwaga. Analogicznie definiuje się różniczkowalność w punkcie funkcji trzech zmiennych. Istnienie pochodnych cząstkowych funkcji w punkcie nie gwarantuje jeszcze różniczkowalności funkcji w tym punkcie.

Tw. 4.2.2 (warunek konieczny różniczkowalności funkcji)

Jeżeli funkcja jest różniczkowalna w punkcie, to jest ciągła w tym punkcie.

Uwaga. Twierdzenie odwrotne nie jest prawdziwe. Świadczy o tym przykład funkcji
, która jest ciągła w punkcie (0,0), ale nie jest w tym punkcie różniczkowalna.

Tw. 4.2.3 (warunek wystarczający różniczkowalności funkcji)

Niech funkcja f będzie określona na otoczeniu punktu (x₀,y₀). Niech ponadto

1. pochodne cząstkowe
,
istnieją na otoczeniu punktu (x₀,y₀),

2. pochodne cząstkowe
,
będą ciągłe w punkcie (x₀,y₀).

Wtedy funkcja f jest różniczkowalna w punkcie (x₀,y₀).

Uwaga. Ostatnie twierdzenie jest prawdziwe także dla funkcji trzech zmiennych.

Fakt 4.2.4 (interpretacja geometryczna funkcji różniczkowalnej w punkcie)

Różniczkowalność funkcji f w punkcie (x₀,y₀) oznacza, że istnieje płaszczyzna styczna (niepionowa) do wykresu tej funkcji w punkcie (x₀,y₀,f(x₀,y₀)).

Rys 4.2.1 Płaszczyzna styczna do wykresu funkcji

Fakt 4.2.5 (równanie płaszczyzny stycznej do wykresu funkcji)

Niech funkcja f będzie różniczkowalna w punkcie (x₀,y₀). Równanie płaszczyzny stycznej do wykresu funkcji f w punkcie (x₀,y₀,z₀), gdzie
, ma postać:

.

Def. 4.2.6 (różniczka funkcji)

Niech funkcja f będzie określona na otoczeniu punktu (x₀,y₀). Ponadto niech funkcja f ma pochodne cząstkowe pierwszego rzędu w punkcie (x₀,y₀). Różniczką funkcji f w punkcie (x₀,y₀) nazywamy funkcję zmiennych
,
określoną wzorem:

.

Różniczkę funkcji f oznacza się także przez df(x₀,y₀) lub krótko df.

Uwaga. Analogicznie definiuje się różniczkę funkcji trzech zmiennych.

Fakt 4.2.7 (zastosowanie różniczki funkcji do obliczeń przybliżonych)

Niech funkcja f będzie różniczkowalna w punkcie (x₀,y₀). Wtedy

.

Uwaga. Prawdziwy jest także analogiczny wzór przybliżony dla funkcji trzech zmiennych. Wzory te wykorzystuje się do obliczeń przybliżonych skomplikowanych wyrażeń algebraicznych.

Fakt 4.2.8 (zastosowanie różniczki funkcji do szacowania błędów pomiarów)

Niech wielkości fizyczne x, y, z będą związane zależnością z = f(x,y). Ponadto niech
i
oznaczają odpowiednio błędy bezwzględne pomiaru wielkości x i y. Wtedy błąd bezwzględny
obliczeń wielkości z wyraża się wzorem przybliżonym:

.

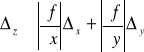
Prawdziwe są także analogiczne wzory dla większej liczby wielkości fizycznych.

4.3 RÓŻNICZKOWANIE FUNKCJI ZŁOŻONYCH

Tw. 4.3.1 (o pochodnej funkcji złożonej)

Niech

1. funkcja f ma ciągłe pochodne cząstkowe
,
na obszarze D ⊂ R²,

2. funkcje x, y będą różniczkowalne na przedziale (a,b) ⊂ R oraz (x(t),y(t)) ∈ D dla każdego t ∈ (a,b).

Wtedy funkcja złożona F(t) = f(x(t),y(t)) jest różniczkowalna na przedziale (a,b) oraz

.

Uwaga. Analogiczna reguła różniczkowania jest prawdziwa dla funkcji trzech zmiennych.

Tw. 4.3.3 (o pochodnych cząstkowych funkcji złożonej)

Niech funkcja f będzie określona na obszarze D ⊂ R² oraz niech funkcje x, y będą określone na obszarze U ⊂ R², przy czym (x(u,v),y(u,v))∈D dla każdego punktu (u,v) ∈ U. Ponadto niech

1. pochodne cząstkowe
,
będą ciągłe na obszarze D,

2. pochodne cząstkowe
,
istnieją na obszarze U.

Wtedy funkcja złożona F(u,v) = f(x(u,v),y(u,v)) ma na obszarze U pochodne cząstkowe pierwszego rzędu wyrażone wzorami:

,
.

Uwaga. Jeżeli f jest funkcją tylko jednej zmiennej, to reguły różniczkowania funkcji F(u,v) = f(x(u,v)) przyjmują postać:

,
.

Analogiczne reguły różniczkowania są prawdziwe także dla funkcji trzech zmiennych.

4.4 POCHODNA KIERUNKOWA FUNKCJI

Def. 4.4.1 (pochodna kierunkowa funkcji)

Niech funkcja f będzie określona na obszarze D ⊂ R² oraz niech punkt (x₀,y₀) ∈ D. Ponadto niech
będzie wersorem na płaszczyźnie. Pochodną kierunkową funkcji f w punkcie (x₀,y₀) w kierunku wersora
określamy wzorem:

.

Fakt 4.4.2 (interpretacja geometryczna pochodnej kierunkowej)

Niech funkcja f będzie określona na otoczeniu punktu (x₀,y₀). Ponadto niech γ oznacza kąt nachylenia do płaszczyzny xOy półstycznej do krzywej otrzymanej w wyniku przekroju wykresu funkcji f półpłaszczyzną przechodzącą przez prostą x = x₀, y = y₀ oraz równoległą do wersora
. Wtedy

.

Pochodna kierunkowa określa szybkość zmiany wartości funkcji f w kierunku wersora
.

Rys 4.4.1 Interpretacja geometryczna pochodnej kierunkowej funkcji

Uwaga. Analogicznie określa się pochodną kierunkową dla funkcji trzech zmiennych. Pochodna kierunkowa jest przeniesieniem na funkcje wielu zmiennych pojęcia pochodnej jednostronnej funkcji jednej zmiennej. Niektórzy autorzy przyjmują, że w definicji pochodnej kierunkowe t dąży do 0 z obu stron. Pochodna kierunkowa jest wtedy uogólnieniem pojęcia pochodnej cząstkowej funkcji. Np. dla funkcji f dwóch zmiennych oraz wersorów
i
mamy

i
.

Def. 4.4.3 (gradient funkcji)

Niech funkcja f będzie określona na obszarze D ⊂ R² oraz niech punkt (x₀,y₀) ∈ D. Ponadto niech istnieją pochodne cząstkowe
,
. Gradientem funkcji f w punkcie (x₀,y₀) nazywamy wektor określony wzorem:

.

Gradient funkcji f oznaczamy także krótko przez gradf. Analogicznie określa się gradient dla funkcji trzech zmiennych.

Tw. 4.4.4 (wzór do obliczania pochodnej kierunkowej)

Niech funkcja f będzie określona na obszarze D ⊂ R². Ponadto niech

1. pochodne cząstkowe
,
istnieją na obszarze D,

2. pochodne cząstkowe
,
będą ciągłe w punkcie (x₀,y₀) ∈ D.

Wtedy

,

gdzie
jest dowolnym wersorem na płaszczyźnie. Podobny wzór do obliczania pochodnej kierunkowej jest prawdziwy także dla funkcji trzech zmiennych.

Fakt. 4.4.5 (interpretacja geometryczna gradientu)

1. Gradient funkcji w punkcie wskazuje kierunek najszybszego wzrostu funkcji w tym punkcie (rys. 4.4.2).

2. Gradient funkcji w punkcie jest prostopadły do poziomicy funkcji przechodzącej przez ten punkt (rys. 4.4.3).

Rys 4.4.2		Rys 4.4.3

4.5 WZÓR TAYLORA. EKSTREMA FUNKCJI

Def. 4.5.1 (różniczka n-tego rzędu funkcji dwóch zmiennych)

Niech funkcja f ma na otoczeniu punktu (x₀,y₀) ciągłe pochodne cząstkowe do rzędu n ∈ N włącznie. Różniczką n-tego rzędu funkcji f w punkcie (x₀,y₀) nazywamy funkcję dⁿf(x₀,y₀) zmiennych Δx i Δy określoną wzorem:

.

We wzorze tym symbole
,
oznaczają operacje różniczkowania po zmiennych x i y, natomiast potęgę traktujemy formalnie do otrzymania pochodnych cząstkowych wyższych rzędów. Różniczkę n-tego rzędu funkcji f oznaczmy krótko przez dⁿf. Dodatkowo przyjmujemy, że
.

Tw. 4.5.2 (wzór Taylora)

Niech funkcja f ma na otoczeniu O punktu (x₀,y₀) ciągłe pochodne cząstkowe do rzędu n ≥ 1 włącznie oraz niech punkt (x₀+x,y₀+y) ∈ O. Wtedy

.

Uwaga. Równość podaną w tezie twierdzenia nazywamy wzorem Taylora dla funkcji dwóch zmiennych. Ostatni składnik we wzorze Taylora nazywamy n-tą resztą tego wzoru i oznaczamy przez R_n. Dla punktu (x₀,y₀) = (0,0) powyższą równość nazywamy wzorem Maclaurina.

Def. 4.5.3 (ekstrema lokalne i wartości ekstremalne funkcji dwóch zmiennych)

Funkcja f ma w punkcie (x₀,y₀) ∈ D_f minimum lokalne, jeżeli

.

Funkcja f ma w punkcie (x₀,y₀) ∈ D_f minimum lokalne właściwe, jeżeli

.

Liczba m jest najmniejszą wartością funkcja f na zbiorze A ⊂ D_f, jeżeli

oraz
.

Funkcja f ma w punkcie (x₀,y₀) ∈ D_f maksimum lokalne, jeżeli

.

Funkcja f ma w punkcie (x₀,y₀) ∈ D_f maksimum lokalne właściwe, jeżeli

.

Liczba M jest największą wartością funkcja f na zbiorze A ⊂ D_f, jeżeli

oraz
.

Tw. 4.5.4 (warunek konieczny istnienia ekstremum)

Niech funkcja f będzie określona na otoczeniu punktu (x₀,y₀). Ponadto niech

1. funkcja f ma ekstremum lokalne w punkcie (x₀,y₀),

2. istnieją pochodne cząstkowe
,

Wtedy

,
.

Uwaga. Z twierdzenia tego wynika, że funkcja może mieć ekstrema tylko w punktach, w których wszystkie jej pochodne cząstkowe są równe 0 albo w punktach, w których choć jedna pochodna cząstkowa nie istnieje. Zerowanie się w punkcie obu pochodnych cząstkowych nie gwarantuje jeszcze istnienia ekstremum lokalnego. Np. funkcja f(x,y) = x³ spełnia równości
,
, ale nie ma ekstremum w punkcie (0,0).

Tw. 4.5.5 (warunek wystarczający istnienia ekstremum)

Niech funkcja f będzie określona na otoczeniu punktu (x₀,y₀). Ponadto niech

1. funkcja f ma ciągłe pochodne cząstkowe rzędu drugiego na otoczeniu punktu (x₀,y₀),

2.
,

3.
.

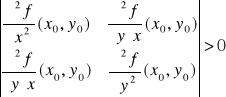
Wtedy funkcja f ma ekstremum lokalne w punkcie (x₀,y₀) i jest to:

a) minimum lokalne właściwe, gdy

b) maksimum lokalne właściwe, gdy
.

Uwaga. Gdy wyznacznik w założeniu 3 powyższego twierdzenia jest ujemny, to funkcja f nie ma w punkcie (x₀,y₀) ekstremum lokalnego. Natomiast, gdy wyznacznik ten jest równy 0, to badanie, czy funkcja f ma ekstremum lokalne w punkcie (x₀,y₀) przeprowadzamy innymi metodami (np. korzystając z definicji).

Def. 4.5.6 (ekstrema warunkowe funkcji)

Funkcja f ma w punkcie (x₀,y₀) minimum lokalne właściwe przy warunku g(x,y) = 0, gdy g(x₀,y₀) = 0 oraz istnieje liczba δ>0 taka, że f(x,y) > f(x₀,y₀) dla każdego punktu (x,y) ∈ S((x₀,y₀),δ) spełniającego warunek g(x,y) = 0.

Funkcja f ma w punkcie (x₀,y₀) maksimum lokalne właściwe przy warunku g(x,y) = 0, gdy g(x₀,y₀) = 0 oraz istnieje liczba δ>0 taka, że f(x,y) < f(x₀,y₀) dla każdego punktu (x,y) ∈ S((x₀,y₀),δ) spełniającego warunek g(x,y) = 0.

Rys 4.5.1 Funkcja f osiąga w punkcie (x0,y0) maksimum przy warunku g(x,y) = 0

Fakt 4.5.7 (algorytm znajdowania ekstremów warunkowych)

Ekstrema lokalne funkcji f dwóch zmiennych z warunkiem g(x,y) = 0 znajdujemy według algorytmu:

1. krzywą L: g(x,y) = 0 (g(x,y) jest podanym warunkiem) dzielimy na łuki, które są wykresami funkcji postaci y = p(x) dla x ∈ I lub x = q(x) dla x ∈ J.

2. szukamy ekstremów funkcji jednej zmiennej f(x,p(x)) na przedziale I lub f(q(y),y) na przedziale J.

3. porównujemy wartości otrzymanych ekstremów na krzywej L i ustalamy ekstrema warunkowe.

Fakt 4.5.8 (algorytm znajdowania wartości ekstremalnych na obszarze domkniętym)

Wartości najmniejszą i największą funkcji na obszarze domkniętym znajdujemy w następujący sposób:

1. wyznaczamy punkty „podejrzane” o ekstrema lokalne zawarte na wnętrzu obszaru,

2. wyznaczamy punkty „podejrzane” o ekstrema lokalne zawarte na brzegu obszaru,

3. wyznaczamy punkty „sklejenia” łuków tworzących brzeg obszaru,

4. obliczamy wartości funkcji we wszystkich otrzymanych punktach i wyznaczamy wartość największą i najmniejszą.

4.6 FUNKCJE UWIKŁANE

Def. 4.6.1 (funkcji uwikłane)

Funkcją uwikłaną określoną przez warunek

nazywamy każdą funkcję y = y(x) spełniającą równość

dla wszystkich x z pewnego przedziału I. Podobnie określa się funkcję uwikłaną postaci x = x(y), gdzie y ∈ J.

Rys 4.6.1 Funkcje uwikłane y = y(x), x ∈ I oraz x = x(y), y ∈ J, określone przez warunek F(x,y) = 0

Tw. 4.6.2 (o istnieniu i różniczkowalności funkcji uwikłanej)

Niech F będzie określona na pewnym otoczeniu punktu (x₀,y₀). Ponadto niech

1. pochodne cząstkowe
   istnieją i są ciągłe na tym otoczeniu,

2. 
   

3. 
   .

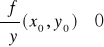
Wtedy na pewnym otoczeniu punktu x₀ istnieje jednoznacznie określona funkcja uwikłana y = y(x) spełniająca warunki:

1. 
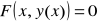
   dla każdego x z tego otoczenia,

2. y(x₀) = y₀,

3. 
   dla każdego x z tego otoczenia.

Uwaga. Jeżeli funkcja F ma ciągłe pochodne cząstkowe drugiego rzędu na otoczeniu punktu (x₀,y₀) oraz spełnia warunki

,

to funkcja uwikłana y = y(x) jest dwukrotnie różniczkowalna na pewnym otoczeniu punktu x₀.

Tw. 4.6.3 (o ekstremach funkcji uwikłanej)

Niech funkcja F będzie określona na otoczeniu punktu (x₀,y₀) i niech ma tam ciągłe pochodne cząstkowe rzędu drugiego. Ponadto niech

1. 
   ,

2. 
   ,

3. 
   .

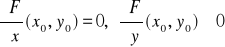
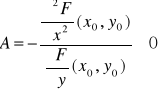
Wtedy funkcja uwikłana y = y(x) określona przez równanie F(x,y) = 0 ma w punkcie (x₀,y₀) ekstremum lokalne właściwe i jest to:

1. minimum, gdy A > 0

2. maksimum, gdy A < 0.

Uwaga. Równość
jest warunkiem koniecznym, a nierówność
jest warunkiem wystarczającym istnienia ekstremum funkcji uwikłanej. Prawdziwe jest także analogiczne twierdzenie o ekstremach funkcji uwikłanej postaci x = x(y).

Fakt 4.6.4 (algorytm znajdowania ekstremów lokalnych funkcji uwikłanej)

1. Punkty, w których funkcja uwikłana może mieć ekstrema, znajdujemy korzystając z warunku koniecznego istnienia ekstremum. W tym celu rozwiązujemy układ warunków:

,
,
.

2. W otrzymanych punktach (x₀,y₀) sprawdzamy warunek wystarczający istnienia ekstremum, tj. określamy znak wyrażenia

.

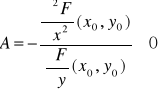
Na podstawie znaku tego wyrażenia ustalamy rodzaj ekstremum.

5. CAŁKI PODWÓJNE

5.1 CAŁKI PODWÓJNE PO PROSTOKCIE

Oznaczenia w definicji całki po prostokącie:

P = {(x,y): a ≤ x ≤ b, c ≤ y ≤ d} - prostokąt na płaszczyźnie;

P = {P₁, P₂, ..., P_n} - podział prostokąt P na prostokąty P_k, 1 ≤ k ≤ n, przy czym prostokąty podziału całkowicie wypełniają ten prostokąt i mają parami rozłączne wnętrza;

Δx_k, Δy_k - wymiary prostokąta P_k, 1 ≤ k ≤ n;

- długość przekątnej prostokąta P_k, 1 ≤ k ≤ n;

δ(P) = max{d_k: 1 ≤ k ≤ n } - średnica podziału P;

, gdzie
, 1 ≤ k ≤ n - zbiór punktów pośrednich podziału P.

Rys 5.5.1 Podział P prostokąta P = [a,b] × [c,d]

Def. 5.1.1 (całka podwójna po prostokącie)

Niech funkcja f będzie ograniczona na prostokącie P. Całkę podwójną z funkcji f po prostokącie P definiujemy wzorem:

,

o ile granica po prawej stronie znaku równości istnieje oraz nie zależy od sposobów podziału P prostokąta P, ani od sposobów wyboru punktów pośrednich Ξ. Mówimy wtedy, że funkcja f jest całkowalna na prostokącie P.

Uwaga. Całkę podwójną z funkcji f po prostokącie P oznaczamy też symbolem
. Całka podwójna po prostokącie jest naturalnym uogólnieniem całki z funkcji jednej zmiennej po przedziale.

Fakt 5.1.2 (o całkowalności funkcji ciągłych)

Funkcja ciągła na prostokącie jest na nim całkowalna.

Tw. 5.1.3 (o liniowości całki)

Jeżeli funkcje f i g są całkowalne na prostokącie P oraz c ∈ R, to:

a) funkcja f + g jest całkowalna na prostokącie P oraz

;

b) funkcja cf jest całkowalna na prostokącie P oraz

.

Tw. 5.1.4 (o addytywności całki względem obszaru całkowania)

Niech funkcja f będzie całkowalna na prostokącie P. Wtedy dla dowolnego podziału prostokąta P na prostokąty P₁, P₂ o rozłącznych wnętrzach funkcja f jest całkowalna na tych prostokątach oraz

.

Tw. 5.1.5 (o zamianie całki podwójnej na całki iterowane)

Niech funkcja f będzie ciągła na prostokącie P = {(x,y): a ≤ x ≤ b, c ≤ y ≤ d}. Wtedy

.

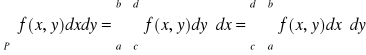
Uwaga. Całki występujące w tezie powyższego twierdzenia nazywamy krótko całkami iterowanymi funkcji f po prostoką­cie P. Będziemy pisali umownie

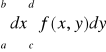
i
,

zamiast odpowiednio

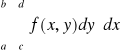
i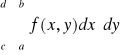
.

Fakt 5.1.6 (całka z funkcji o rozdzielonych zmiennych)

Jeżeli

1. funkcja g jest ciągła na przedziale [a,b],

2. funkcja f jest ciągła na przedziale [c,d],

to

,

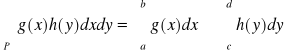
gdzie P = [a,b] × [c,d].

5.2 CAŁKI PODWÓJNE PO OBSZARACH NORMALNYCH

Def. 5.2.1 (całka podwójna po obszarze)

Niech funkcja f będzie funkcją ograniczoną na obszarze ograniczonym D ⊂ R² oraz niech P będzie dowolnym prostokątem zawierającym obszar D. Ponadto niech f^* oznacza rozszerzenie funkcji f na R² określone wzorem:

.

Całkę podwójną funkcji f po obszarze D definiujemy wzorem:

,

o ile całka po prawej stronie znaku równości istnieje. Mówimy wtedy, że funkcja f jest całkowalna na obszarze D.

Uwaga. Całka
nie zależy od wyboru prostokąta P.

Def. 5.2.2 (obszary normalne względem osi układu)

a) Obszarem normalnym względem osi Ox nazywamy zbiór

,

gdzie funkcje g i h są ciągłe na [a,b] oraz g(x) < h(x) dla każdego x ∈ (a,b).

b) Obszarem normalnym względem osi Oy nazywamy zbiór

,

gdzie funkcje p i q są ciągłe na [c,d] oraz p(y) < q(y) dla każdego y ∈ (c,d).

Rys 5.2.1 Obszar normalny względem osi Ox			Rys 5.2.2 Obszar normalny względem osi Oy

Tw. 5.2.3 (całki iterowane po obszarach normalnych)

a) Jeżeli funkcja f jest ciągła na obszarze normalnym
, to

.

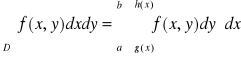
b) Jeżeli funkcja f jest ciągła na obszarze normalnym
, to

.

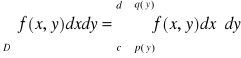
Uwaga. Całki iterowane:

,

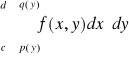
będziemy zapisywali umownie odpowiednio w postaci:

,
.

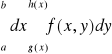
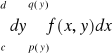
Def. 5.2.4 (obszar regularny na płaszczyźnie)

Sumę skończonej liczby obszarów normalnych (względem osi Ox lub Oy) o parami rozłącznych wnętrzach nazywamy obszarem regularnym na płaszczyźnie.

Fakt 5.2.5 (całka po obszarze regularnym)

Niech obszar regularny D będzie sumą obszarów normalnych D₁, D₂, ..., D_n o parami rozłącznych wnętrzach oraz niech funkcja f będzie całkowalna na obszarze D. Wtedy

.

Uwaga. Całki po obszarach regularnych mają te same własności, co całki po prostokątach (liniowość, addytywność względem obszaru całkowania).

Def. 5.2.6 (całka podwójna z funkcji wektorowej)

Niech funkcje P, Q będą całkowalne na obszarze regularnym D ⊂ R². Całkę z funkcji wektorowej
po obszarze D określamy wzorem:

.

Uwaga. Podobnie definiuje się całkę po obszarze D z funkcji wektorowej postaci:
.

Tw. 5.2.7 (o całkowaniu funkcji nieciągłych)

Jeżeli

1. funkcja f jest całkowalna na obszarze regularnym D,

2. funkcja ograniczona g pokrywa się z funkcją f poza skończoną liczbą krzywych, które są wykresami funkcji ciągłych postaci y = p(x) lub x = q(y),

to funkcja g jest całkowalna na D oraz

.

Def. 5.2.8 (wartość średnia funkcji na obszarze)

Wartością średnią funkcji f na obszarze D nazywamy liczbę:

,

gdzie |D| oznacza pole obszaru D.

Tw. 5.2.9 (o wartości średniej dla całek podwójnych)

Niech funkcja f będzie ciągła na obszarze normalnym D. Wtedy

.

5.3 ZAMIANA ZMIENNYCH W CAŁKACH PODWÓJNYCH

Def. 5.3.1 (współrzędne biegunowe)

Położenie punktu P na płaszczyźnie można opisać parą liczb (ϕ,ρ), gdzie:

ϕ - oznacza miarę kąta między dodatnią częścią osi Ox a promieniem wodzącym punktu P,
albo
;

ρ - oznacza odległość punktu P od początku układu współrzędnych,
.

Fakt 5.3.2 (zależność między współrzędnymi biegunowymi i kartezjańskimi)

Współrzędne kartezjańskie (x,y) punktu płaszczyzny danego we współrzędnych biegunowych (ϕ,ρ) określone są wzorami:

.

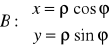
Rys. 5.3.1 Ilustracja do wzorów na przejście od współ-rzędnych biegunowych do kartezjańskich

Tw. 5.3.3 (współrzędne biegunowe w całce podwójnej)

Niech

1. obszar U będzie określony we współrzędnych biegunowych wzorem:

,

gdzie funkcje g i h są ciągłe na przedziale [α,β] ⊂ [0,2π],

2. funkcja f będzie ciągła na obszarze D, który jest obrazem obszaru U przy przekształceniu biegunowym, D = B(U).

Wtedy

.

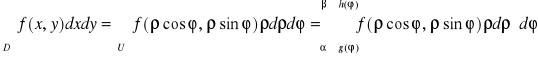
Uwaga. Całkę iterowaną

będziemy zapisywali umownie w postaci

.

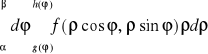
5.4 ZASTOSOWANIA CAŁEK PODWÓJNYCH

Fakt 5.4.1 (zastosowania w geometrii)

1. Pole obszaru D ⊂ R² wyraża się wzorem:

2. Objętość bryły V położonej nad obszarem D ⊂ R² i ograniczonej powierzchniami z = d(x,y) i z = g(x,y) (rys. 5.4.1), wyraża się wzorem:

.

3. Pole płata Σ, który jest wykresem funkcji z = f(x,y), gdzie (x,y) ∈ D (rys. 5.4.2), wyraża się wzorem:

.

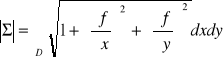
Zakładamy tu, że funkcja f ma ciągłe pochodne cząstkowe pierwszego rzędu na obszarze D.

Rys 5.4.1		Rys 5.4.2

Fakt 5.4.2 (zastosowania w fizyce)

1. Masa obszaru D o gęstości powierzchniowej masy σ wyraża się wzorem:

.

2. Momenty statyczne względem osi Ox i Oy obszaru D o gęstości powierzchniowej masy σ wyrażają się wzorami:

,
.

3. Współrzędne środka masy obszaru D o gęstości powierzchniowej masy σ wyrażają się wzorami:

,

4. Momenty bezwładności względem osi Ox, Oy oraz punktu O obszaru D o gęstości powierzchniowej masy σ wyrażają się wzorami:

,

.

5. Parcie P na jedną stronę płaskiej płytki D zanurzonej pionowo w cieczy o ciężarze właściwym γ wyraża się wzorem:

.

6. Natężenie pola elektrycznego indukowane w punkcie
przez ładunek elektryczny o gęstości powierzchniowej ładunku σ, rozłożony w sposób ciągły na obszarze D, wyraża się wzorem:

,

gdzie
, a ε₀ oznacza przenikalność elektryczną próżni.

7. Siła przyciągania grawitacyjnego masy m skupionej w punkcie
przez obszar D o gęstości powierzchniowej masy σ wyraża się wzorem:

,

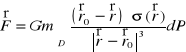
gdzie
, a G oznacza stałą grawitacji.

8. Energia kinetyczna obszaru D o gęstości powierzchniowej masy σ, obracającego się z prędkością kątową ω wokół osi Oy, wyraża się wzorem:

.

Uwaga. Wzór na natężenie pola grawitacyjnego jest analogiczny do wzoru na natężenie pola elektrycznego. Wzór na siłę przyciągania pochodzącą od ładunków elektrycznych jest analogiczny do wzoru na siłę przyciągania grawitacyjnego. Wzory te są prawdziwe także dla obszarów płaskich położonych w przestrzeni. Wtedy przyjmujemy
oraz
.

Fakt 5.4.3 (środki masy obszarów symetrycznych)

1. Gdy obszar na płaszczyźnie ma środek symetrii i gęstość powierzchniowa jest funkcją symetryczną względem tego środka (np. jest stała), to środek masy obszaru pokrywa się z jego środkiem symetrii.

2. Gdy obszar na płaszczyźnie ma oś symetrii i gęstość powierzchniowa jest funkcją symetryczną względem tej osi (np. jest stała), to środek masy obszaru leży na tej osi.

Fakt 5.4.4 (I reguła Guldina)

Niech S będzie figurą ograniczoną zawartą w półpłaszczyźnie. Objętość bryły V powstałej z obrotu figury S wokół krawędzi półpłaszczyzny wyraża się wzorem:

,

gdzie r_C oznacza odległość środka masy figury S od osi obrotu, a |S| oznacza pole tej figury.

Fakt 5.4.5 (II reguła Guldina)

Niech L będzie krzywą ograniczoną zawartą w półpłaszczyźnie. Pole powierzchni Σ powstałej z obrotu krzywej L wokół krawędzi półpłaszczyzny wyraża się wzorem:

,

gdzie r_C oznacza odległość środka masy krzywej L od osi obrotu, a |L| oznacza długość tej krzywej.

6. CAŁKI POTRÓJNE

6.1 CAŁKI POTRÓJNE PO PROSTOPADŁOŚCIANIE

Oznaczenia w definicji całki po prostopadłościanie:

P = {(x,y,z): a ≤ x ≤ b, c ≤ y ≤ d, p ≤ z ≤ q} - prostopadłościan w przestrzeni;

P = {P₁, P₂, ..., P_n} - podział prostopadłościanu P na prostopadłościany P_k, 1 ≤ k ≤ n, przy czym prostopadłościany podziału całkowicie wypełniają prostopadłościan P i mają parami rozłączne wnętrza;

Δx_k, Δy_k, Δz_k - wymiary prostopadłościanu P_k, 1 ≤ k ≤ n;

- długość przekątnej prostopadłościanu P_k, 1 ≤ k ≤ n;

δ(P) = max{d_k: 1 ≤ k ≤ n } - średnica podziału P;

, gdzie
, 1 ≤ k ≤ n - zbiór punktów pośrednich podziału P.

Rys 6.6.1 Podział P prostopadłościanu P = [a,b] × [c,d] × [p,q]

Def. 6.1.1 (całka potrójna po prostopadłościanie)

Niech funkcja f będzie ograniczona na prostopadłościanie P. Całkę podwójną z funkcji f po prostopadłościanie P definiujemy wzorem:

,

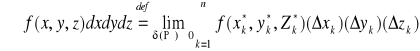
o ile granica po prawej stronie znaku równości istnieje oraz nie zależy od sposobów podziału P prostopadłościanu P, ani od sposobów wyboru punktów pośrednich Ξ. Mówimy wtedy, że funkcja f jest całkowalna na prostopadłościanie P.

Uwaga. Całkę potrójną z funkcji f po prostopadłościanie P oznaczamy też symbolem
.

Fakt 6.1.2 (o całkowaniu funkcji ciągłej)

Funkcja ciągła na prostopadłościanie jest na nim całkowalna.

Tw. 6.1.3 (o liniowości całki)

Jeżeli funkcje f i g są całkowalne na prostopadłościanie P oraz c ∈ R, to:

a) funkcja f + g jest całkowalna na prostopadłościanie P oraz

;

b) funkcja cf jest całkowalna na prostopadłościanie P oraz

.

Tw. 6.1.4 (o addytywności względem obszaru całkowania)

Jeżeli funkcja f jest całkowalna na prostopadłościanie P, to dla dowolnego podziału prostopadłościanu P na dwa prostopadłościany P₁, P₂ o rozłącznych wnętrzach, funkcja f jest całkowalna P₁ i P₂ na oraz

.

Tw. 6.1.5 (o zamianie całki potrójnej na całkę iterowaną)

Jeżeli funkcja f jest ciągła na prostopadłościanie P = {(x,y,z): a ≤ x ≤ b, c ≤ y ≤ d, p ≤ z ≤ q}, to

.

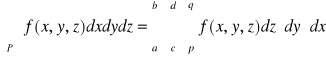
Uwaga. Powyższe twierdzenie będzie prawdziwe także wtedy, gdy po prawej stronie równości napiszemy dowolną inną całkę iterowaną (jest sześć rodzajów całek iterowanych). Całkę iterowaną

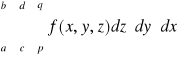
zapisujemy umownie w postaci

.

Podobną umowę przyjmujemy dla pozostałych całek iterowanych. W wielu przypadkach wybór odpowiedniej kolejności całkowania pozwala znacznie uprościć obliczenia całki potrójnej.

Fakt 6.1.6 (całka z funkcji o rozdzielonych zmiennych)

Jeżeli

1. funkcja f jest ciągła na przedziale [a,b],

2. funkcja g jest ciągła na przedziale [c,d],

3. funkcja h jest ciągła na przedziale [p,q],

to

,

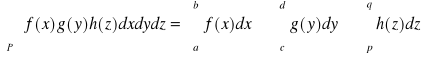
gdzie P = [a,b] × [c,d] × [p,q].

6.2 CAŁKI POTRÓJNE PO OBSZARACH NORMALNYCH

Def. 6.2.1 (całka potrójna po obszarze)

Niech funkcja f będzie funkcją ograniczoną na obszarze ograniczonym V ⊂ R³ oraz niech P będzie dowolnym prostopadłościanem zawierającym obszar V. Ponadto niech f^* oznacza rozszerzenie funkcji f na R³ określone wzorem:

.

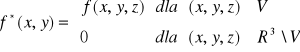
Całkę potrójną funkcji f po obszarze V definiujemy wzorem:

,

o ile całka po prawej stronie znaku równości istnieje. Mówimy wtedy, że funkcja f jest całkowalna na obszarze V.

Uwaga. Całka
nie zależy od wyboru prostopadłościanu P.

Def. 6.2.2 (obszary normalne względem płaszczyzn układu)

a) Obszarem normalnym względem osi xOy nazywamy zbiór

,

gdzie U jest obszarem regularnym na płaszczyźnie xOy, a funkcje D i G są ciągłe na U, przy czym D(x,y) < G(x,y) dla punktów (x,y) należących do wnętrza obszaru U.

b) Obszarem normalnym względem osi xOz nazywamy zbiór

,

gdzie U jest obszarem regularnym na płaszczyźnie xOz, a funkcje D i G są ciągłe na U, przy czym D(x,z) < G(x,z) dla punktów (x,z) należących do wnętrza obszaru U.

c) Obszarem normalnym względem osi yOz nazywamy zbiór

,

gdzie U jest obszarem regularnym na płaszczyźnie yOz, a funkcje D i G są ciągłe na U, przy czym D(y,z) < G(y,z) dla punktów (y,z) należących do wnętrza obszaru U.

Rys 6.2.1 Obszar normalny względem płaszczyzny xOy	Rys 6.2.2 Obszar normalny względem Płaszczyzny xOz	Rys 6.2.3 Obszar normalny względem płaszczyzny yOz

Tw. 6.2.3 (całki iterowane po obszarach normalnych)

Jeżeli funkcja f jest ciągła na obszarze
normalnym względem płaszczyzny xOy, gdzie D i G są ciągłe na obszarze regularnym U, to

.

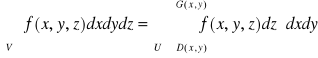
Jeżeli funkcja f jest ciągła na obszarze
normalnym względem płaszczyzny xOy, gdzie funkcje d i g są ciągłe na odcinku [a,b], a funkcje D i G są ciągłe na obszarze
, to

.

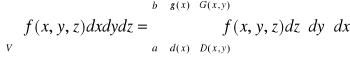
Uwaga. Całkę po prawej stronie powyższej równości będziemy zapisywali umownie w postaci:

.

Prawdziwe są także analogiczne wzory z całkami iterowanymi po obszarach normalnych względem pozostałych płaszczyzn układu.

Def. 6.2.4 (obszar regularny w przestrzeni)

Sumę skończonej liczby obszarów normalnych względem płaszczyzn układu o parami rozłącznych wnętrzach nazywamy obszarem regularnym w przestrzeni.

Fakt 6.2.5 (całka po obszarze regularnym w przestrzeni)

Niech obszar regularny V będzie sumą obszarów normalnych V₁, V₂, ..., V_n o parami rozłącznych wnętrzach oraz niech funkcja f będzie całkowalna na obszarze V. Wtedy

.

Uwaga. Całki po obszarach regularnych mają te same własności co całki po prostopadłościanach (liniowość, addytywność względem obszaru całkowania).

Def. 6.2.6 (całka potrójna z funkcji wektorowej)

Niech funkcje P, Q, R będą całkowalne na obszarze regularnym V ⊂ R³. Całkę z funkcji wektorowej
po obszarze V określamy wzorem:

.

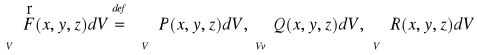
Def. 6.2.7 (wartość średnia funkcji na obszarze)

Wartością średnią funkcji f na obszarze V nazywamy liczbę:

,

gdzie |V| oznacza pole obszaru V.

Tw. 5.2.8 (o wartości średniej dla całek potrójnych)

Jeżeli funkcja f jest ciągła na obszarze normalnym V, to

.

6.3 ZAMIANA ZMIENNYCH W CAŁKACH POTRÓJNYCH

Def. 6.3.1 (współrzędne walcowe)

Położenie punktu P w przestrzeni można opisać trójką liczb (ϕ,ρ,h), gdzie:

ϕ - oznacza miarę kąta między rzutem promienia wodzącego punktu P na płaszczyznę xOy, a dodatnią częścią osi Ox,
albo
;

ρ - oznacza odległość punktu P od początku układu współrzędnych,
,

h - oznacza odległość (dodatnią lub ujemną) punktu P od płaszczyzny xOy,
.

Rys 6.3.1 Współrzędne walcowe punktu w przestrzeni

Fakt 6.3.2 (zamiana współrzędnych walcowych na kartezjańskie)

Współrzędne kartezjańskie (x,y,z) punktu przestrzeni danego we współrzędnych walcowych (ϕ,ρ,h) określone są wzorami:

.

Rys. 6.3.2 Zamiana współrzędnych walcowych na kartezjańskie

Tw. 6.3.3 (współrzędne walcowe w całce potrójnej)

Niech

1. Obszar U będzie określony we współrzędnych walcowych wzorem

,

gdzie funkcje d i g są ciągłe na przedziale [α,β[ ⊂ [0,2π], a funkcje D i G są ciągłe ma obszarze

,

2. funkcja f będzie ciągła na obszarze V, który jest obrazem obszaru U przy przekształceniu walcowym, V = W(U).

Wtedy

.

Uwaga. Całkę iterowaną z powyższego twierdzenia zapisujemy umownie w postaci:

.

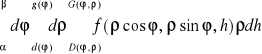
Współrzędne walcowe stosujemy głównie wtedy, gdy obszar całkowania jest ograniczony fragmentami powierzchni walców, sfer, stożków lub płaszczyzn.

Def. 6.3.4 (współrzędne sferyczne)

Położenie punktu P w przestrzeni można opisać trójką liczb (ϕ,ψ,ρ), gdzie

ϕ - oznacza miarę kąta między rzutem promienia wodzącego punktu P na płaszczyznę xOy, a dodatnią częścią osi Ox,
albo
;

ψ - oznacza miarę kąta między promieniem wodzącym punktu P, a płaszczyzną xOy,
,

ρ - oznacza odległość punktu P od początku układu współrzędnych,
.

Uwaga. We współrzędnych geograficznych na Ziemi liczby ϕ, ψ są odpowiednio długością i szerokością geograficzną.

Rys. 6.3.3 Współrzędne sferyczne punktu w przestrzeni

Fakt 6.3.5 (zamiana współrzędnych sferycznych na kartezjańskie)

Współrzędne kartezjańskie punktu (x,y,z) w przestrzeni danego we współrzędnych sferycznych (ϕ,ψ,ρ) określone są wzorami:

.

Rys. 6.3.4 Zamiana współrzędnych sferycznych na kartezjańskie

Tw. 6.3.6 (współrzędne sferyczne w całce potrójnej)

Niech

1. Obszar U będzie określony we współrzędnych sferycznych wzorem

,

gdzie funkcje d i g są ciągłe na przedziale [α,β[ ⊂ [0,2π], a funkcje D i G są ciągłe ma obszarze

,

2. funkcja f będzie ciągła na obszarze V, który jest obrazem obszaru U przy przekształceniu sferycznym, V = S(U).

Wtedy

.

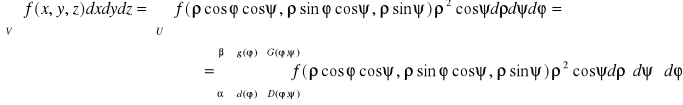
Uwaga. Całkę iterowaną z powyższego twierdzenia zapisujemy umownie w postaci:

.

Współrzędne sferyczne stosujemy głównie do opisu obszarów całkowania, które są ograniczone fragmentami powierzchni sfer, stożków lub płaszczyzn.

6.4 ZASTOSOWANIA CAŁEK POTRÓJNYCH

Fakt 6.4.1 (zastosowania w geometrii)

Objętość obszaru V ⊂ R³ wyraża się wzorem:

.

Fakt 6.4.2 (zastosowania w fizyce)

1. Masa obszaru V ⊂ R³ o gęstości objętościowej masy γ wyraża się wzorem:

.

2. Momenty statyczne względem płaszczyzn układu współrzędnych obszaru V ⊂ R³ o gęstości objętościowej masy γ wyrażają się wzorami:

.

3. Współrzędne środka masy obszaru V ⊂ R³ o gęstości objętościowej masy γ wyrażają się wzorami:

.

4. Momenty bezwładności względem osi układu współrzędnych obszaru V ⊂ R³ o gęstości objętościowej masy γ wyrażają się wzorami:

,

,

.

5. Moment bezwładności względem początku układu współrzędnych obszaru V ⊂ R³ o gęstości objętościowej masy γ wyraża się wzorem:

.

6. Siła przyciągania grawitacyjnego masy m skupionej w punkcie
przez obszar V ⊂ R³ o gęstości objętościowej masy γ wyraża się wzorem:

,

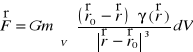
gdzie
, a G oznacza stałą grawitacji.

7. Natężenie pola elektrycznego indukowane w punkcie
przez ładunek elektryczny rozłożony z gęstością objętościową ładunku γ na obszarze V ⊂ R³, wyraża się wzorem:

,

gdzie
, a ε₀ oznacza przenikalność elektryczną próżni.

8. Energia potencjalna względem płaszczyzny xOy obszaru V ⊂ R³ o gęstości objętościowej masy γ wyraża się wzorem:

,

gdzie g oznacza przyspieszenie ziemskie. Zakładamy tutaj, że pole grawitacyjne jest jednorodne.

9. Energia kinetyczna obszaru V ⊂ R³ o gęstości objętościowej masy γ, obracającego się z prędkością kątową ω wokół osi Oz, wyraża się wzorem:

.

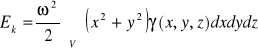
Uwaga. Wzór na siłę przyciągania elektrycznego oraz natężenie pola grawitacyjnego są podobne do podanych wyżej.

Fakt 6.4.3 (środki masy brył symetrycznych)

1. Jeżeli bryła w przestrzeni ma płaszczyznę symetrii i gęstość objętościowa masy jest funkcją symetryczną względem tej płaszczyzny (np. jest stała), to środek masy bryły leży na tej płaszczyźnie.

2. Jeżeli bryła w przestrzeni ma oś symetrii i gęstość objętościowa masy jest funkcją symetryczną względem tej osi (np. jest stała), to środek masy bryły leży na tej osi.

3. Jeżeli bryła w przestrzeni ma środek symetrii i gęstość objętościowa masy jest funkcją symetryczną względem tego środka (np. jest stała), to środek masy bryły pokrywa się ze środkiem symetrii.

z = x² - y²

---