Celem naszego ćwiczenia było zapoznanie się z metodami newtonowskimi i metodą funkcji kary. Kroki przebiegu ćwiczenia:

1. analityczne wyznaczenie minimum globalnego funkcji przy braku ograniczeń

2. wprowadzenie algorytmu w środowisku Matlab

3. testowanie programu dla zróżnicowanych danych

4. porównanie wyników-wnioski

Metoda Newtona-Raphsona

f(x₁,x₂)=(x₁+2)²+(x₂+1)²+(x₁+2)⁴+(x₂+1)⁴+3(x₁+2)(x₂+1)

x_min=[-1.5;-1.5]

Analityczne znalezienie minimum funkcji.

Dla jasności obliczeń przyjęto x₁=x i x₂=y.

Hesjan funkcji ma postać:

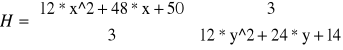
Punkty krytyczne wyznacza się z następującego układu równań:

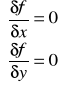
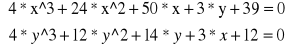
Rzeczywistym rozwiązaniem powyższego układu równań jest punkt (-2,-1) oraz (-1.5, -1.5).

Po podstawieniu do hesjanu otrzymujemy:

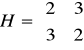
dla punktu (-2, -1). Hesjan jest ujemnie określony, a więc punkt (-2,-1) jest maksimum funkcji.

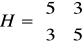
dla punktu (-1.5, -1.5). Hesjan jest dodatnio określony, a więc punkt (-1.5, -1.5) jest minimum funkcji.

Kod programu:

//////////////////////////

function [Xopt, i] = newton(X1, n, eps)

for i=1:n

G=[(2*(X1(1,1) + 2) + 4*(X1(1,1) + 2)^3 + 3*X1(2,1) + 3); (2*(X1(2,1) + 1) + 4*(X1(2,1) + 1)^3 + 3*X1(1,1) + 6)];

H=[(50 + 12*(X1(1,1)^2) + 48*X1(1,1)) 3;3 (14 + 12*(X1(2,1))^2 +24*X1(2,1))];

Xopt = X1 - inv(H)*G;

if (abs(Xopt-X1) < eps)

break;

end

X1=Xopt;

i=i;

end

end

///////////////////////////

Zależność prędkości działania ( ilości iteracji ) od punktu startowego:

Lp.	Punkt startowy x0	Ilość iteracji	Dokładność
1	[2;2]	9
2	[100;50]	18
3	[-2;-2]	7
4	[1000;-300]	22	0.001
5	[-1.2;-1.3]	5
6	[2000;500]	24
7	[5;5]	10
8	[2;2]	10
9	[100;50]	18
10	[-2;-2]	7
11	[1000;-300]	23	0.0001
12	[-1.2;-1.3]	5
13	[2000;500]	25
14	[5;5]	10

Zależność prędkości działania ( ilości iteracji ) od dokładności:

Lp.	Dokładność	Ilość iteracji	Punkt startowy x0
1	0.1	6
2	0.01	7
3	0.001	8	[1;1]
4	0.0001	9
5	0.0000001	9
6	0.1	15
7	0.01	16
8	0.001	17	[100;-100]
9	0.0001	17
10	0.0000001	18

Metoda funkcji kary

//////////////////////////

function[Xmin]=kara(X1,eps,delta)

global r;

f=1000; %przykladowa wartosc poczatkowa dla ktorej nie spelniony jest warunek w while

f0=1; %przykladowa wartosc poczatkowa dla ktorej nie spelniony jest warunek w while

k=0;

warning off; % wylaczenie ostrzezen

while abs(f-f0)>eps

f0=(X1(1,1)+2)^2+(X1(2,1)+1)^2+(X1(1,1)+2)^4+(X1(2,1)+1)^4+3.*(X1(1,1)+2).*(X1(2)+1)-r.*(1./(X1(2,1)-10));

Xmin=fminunc(@(X1)(X1(1,1)+2)^2+(X1(2,1)+1)^2+(X1(1,1)+2)^4+(X1(2,1)+1)^4+3.*(X1(1,1)+2).*(X1(2)+1)-r.*(1./(X1(2,1)-10)),X1);

r=r./delta;

f=(X1(1,1)+2)^2+(X1(2,1)+1)^2+(X1(1,1)+2)^4+(X1(2,1)+1)^4+3.*(X1(1,1)+2).*(X1(2)+1)-r.*(1./(X1(2,1)-10));

k=k+1;

end

k %ilość iteracji

///////////////////////////////

Lp.	Punkt startowy x0	Delta	Wsp. kary	Ilość iteracji
1	[0;0]	2	200	18
2				5		9
3				10		7
4				40		5
5				100		4
6				1.5		29
7			2	1	10
8					2	11
9					10	14
10					100	17
11					250	18
12					500	19
13					1000	20

Wnioski:

• W metodzie Newtona-Raphsona da się zauważyć istnienie zależności ilości iteracji od położenia punktu początkowego - im bardziej oddalony od minimum funkcji jest punkt początkowy tym większa będzie ilość iteracji,

• W zależności od położenia punktu początkowego ilość iteracji może wzrosnąć nawet czterokrotnie - jednakże dla badanej funkcji ilość iteracji w każdym przypadku była niewielka,

• Zależność ilości iteracji od dokładności jest w przybliżeniu liniowa, wraz ze wzrostem dokładności rośnie ilość iteracji, a jednocześnie szybko zostaje osiągnięta maksymalna ilość iteracji,

• Program obliczający minimum za pomocą metody kary działa prawidłowo, kiedy wybieramy ograniczenie zawierające w sobie punkt obliczony wcześniej metodą Newtona. Ilość iteracji spada im szybciej maleje współczynnik kary. Dla jednakowej delty, zwiększając współczynnik kary potrzeba więcej iteracji do osiągnięcia wyniku.

• Nie było możliwe zbadanie metody kary dla aktywnego ograniczenia nierównościowego z powodu budowy tej metody, podczas optymalizacji programowi „opłaca się” wyjść poza obszar dopuszczalny co za tym idzie w przypadku ograniczeń nierównościowych otrzymany punkt leżał poza obszarem dopuszczalnym, było to także spowodowane wartością współczynników funkcji. Matlab zwraca następujący komunikat: „Line search cannot find an acceptable point along the current search direction.”

5

---