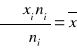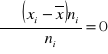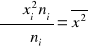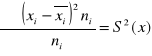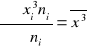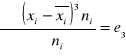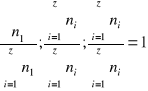Statystyka

Wykład drugi

Analiza struktury dotyczy:

1. Analizy tendencji centralnej w oparciu

• - średnie klasyczne (wyliczane ze wszystkich jednostek badanej próby)

• - średnie pozycyjne (wyliczane z niektórych pozycji)

2. Analiza zróżnicowania w oparciu o miary zróżnicowania(wartości zmiennej, rozproszenie dyspozycji)

3. Analiza skośności w oparciu o miary skośności (asymetrii)

4. Analizy nierównomiernego rozkładu wartości zmiennej na 1 liczebność w oparciu o miary koncentracji

Ad1. Analiza tendencji centralnej

Średnie klasyczne:

- średnia arytmetyczna (zwykła i ważona)

- średnia harmoniczna

- średnia geometryczna

Średnie pozycyjne

- dominanta

- mediana

- kwartyla

Wzór interpolacyjny - zakładamy, że w danej klasie wartości cechy jest linową funkcją zależności, wtedy mediana jest liczona wg wzoru:

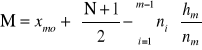
b - liczba charakterystyk v - liczba części

v-1=b

b =3 - kwartyle, b=9 decyle, b=100 centyle

Charakterystyka jest zależna od podziału populacji na klasy.

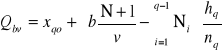
Dzieląc liczbę Skumulowanej liczebności (S) otrzymujemy medianę

D=M=
D>M>
D<M<

Analiza jednej cechy - analiza rozproszenia (dyspersji)

Miary dzielimy na:

Miary absolutne - wyrażone w tych samych miarach co cecha

Względne (stosunkowe) wyrażone………………………..

Wynikowe - decydują wszystkie wartości cech

Pozycyjne - decydują niektóre wartości cech

WARIANCJA

Mamy szereg: x₁, x₂, …… x_z

liczebność: n₁,nx₂, …… n_z

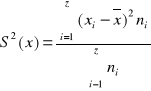
Cechy wariancji:

1. Wartość nie zależy od wartości absolutnych, lecz od ich wag.

2. Rozwijamy wzór

S²(x)=

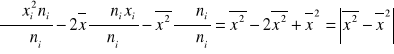
3. Jeżeli populację podzielimy na podpopulację i obliczymy
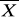
   i wariancje, wtedy okaże się, że wariancja jest równa ????????. Wariancje szeregu całkowitego staje się średnią arytmetyczną.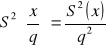

4. 
   

Wada wariancji - jeżeli badamy wzrost cen to wariancja będzie w cm²

Odchylenie standardowe - pierwiastek wariancji

Miary wynikowe

Właściwa miara statystyczna to odchylenie standardowe

Poprawka Sheparda

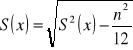
Odchylenie przeciętne

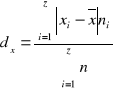
MIARY POZYCYJNE

1. ROZSTĘP

L=x_max-x_min mówi, jaka jest różnica pomiędzy wartością maksymalną a minimalną

Rozstęp uzależniony jest od wartości skrajnych.

Rozstęp jest dobrą miarą przy równomiernym rozkładzie cechy

2. OCHYLENIE ĆWIARTKOWE

3. Względna miara rozproszenia - współczynnik zmienności pozwala porównać populacje lub cechy w populacjach

(wyrażany w %)

MIARY ASYMETRII (SKOŚNOŚCI)

Asymetrią rozkładu cechy w populacji nazywamy sytuację, w której jednostki populacji są rozłożone nierównomiernie ani symetrycznie, zatem skupiają się wokół odmian wyższych lub niższych - Asymetria rozkładu

Siła asymetrii - lewo lub prawo stronna (mierzona wg ogona)

Miary asymetrii:

Współczynnik skośności (Pearsona) - dodatni, ujemny, zero - równomiernie rozłożony.

S(x) - liczba odchyleń standardowych

Współczynnik asymetrii:

e₃ - moment centralny 3 rzędu

S³ odchylenie standardowe do ³ potęgi

Moment w statystyce nazywamy

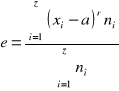
r- rząd momentu

1. rodzaj momentu

2. jeśli a=0 to mówimy o momentach zwykłych

3. zwykłych, jeśli a=
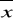
   mówimy o momentach centralnych

	A=0	a=
r=1
r=2		Wariancja
r=3

teoretycznie

praktycznie

Miary koncentracji

X₁, x₂, … x_z Szereg statystyczny

N₁, n₂, … n_z

Koncentracja będzie rozkładem sum wartości cechy pomiędzy jednostki liczebności

Tworzymy iloraz

1. 
   

2.

,

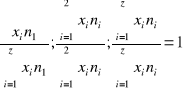
K jest na ogół wyrażany w %

Miary dwóch i więcej cech

- jak liczyć współzależność cech - badanie korelacji lub regresu

Związki funkcyjne - jedna zmienna determinuje wartości innej zmiennej

Związek stochastyczny

Cech x - cecha niezależna, objaśniająca

Cecha y - cecha zależna, objaśniana

Jeżeli odmianie x odpowiadają różne y - to taki związek nazywamy związkiem stochastycznym

Np. 1 ha daje różne plony (w sumie jest np. 10 poletek)

Związek stochastyczny jest opisywany przez tablicę korelacyjną

Xi	Yj
		Y1	Y2	…		Yu
X1	N11	N12		Niu
X2	N21	N22	…	N2u
…	…	…	…	…	…
Xz	Nz1	nzz	…	nzu
			…

Dla każdego szeregu cząstkowego możemy obliczyć średnie arytmetyczne. Wszystkie średnie są sobie równe - dla cechy objaśniającej

Związek korelacyjny - taki związek cech, gdzie odmianom cechy niezależnej odpowiadają różne średnie arytmetyczne cechy objaśnianej.

Statystyka Wykłady 2002-11-12, 9:16

6

M

S

Lewostronna -

Prawostronna +

a

b

---