PROGNOZOWANIE I SYMULACJE
Adaptacyjne metody prognozowania
A) Szeregi ze stałym poziomem zmiennej prognozowanej.
Zadanie 1 (Metoda naiwna)
Wielkość sprzedaży pewnego przedsiębiorstwa produkującego soki owocowe w kolejnych kwartałach 2001-2003 w tys. litrów, przedstawia się następująco:
155 |
162 |
158 |
149 |
152 |
150 |
158 |
154 |
148 |
153 |
158 |
152 |
Zdecyduj, czy do prognozowania wielkości sprzedaży przedsiębiorstwa na I kwartał 2004 roku można zastosować metodę naiwną.
Wyznacz prognozę na I kwartał 2004 metodą naiwną.
Oceń trafność prognozy, jeżeli wiadomo, że rzeczywista wartość sprzedaży w okresie prognozowanym wynosiła 159 tys. litrów.
Zadanie 2 (Metoda średniej ruchomej)
Zużycie środków piorących w pewnym województwie (w kg/os) w latach 1986-1997 przedstawia się następująco:
8,0 |
7,6 |
7,7 |
8,0 |
7,7 |
8,3 |
8,6 |
7,8 |
7,8 |
7,7 |
8,2 |
8,4 |
Odchylenie standardowe w tym szeregu wynosi 0,32 kg/osobę.
Określ, czy wahania przypadkowe w tym szeregu są na tyle małe, że można zastosować metodę średniej ruchomej.
Prognozę zużycia środków piorących wyznacz 3- i 4 -elementową średnią ruchomą prostą oraz 3-elementową średnią ruchomą ważona przyjmując trzy zestawy wag:
I: 0,2 0,3 0,5
II: 0,15 0,25 0,6
III: 0,1 0,2 0,7
Dla każdej prognozy wyznacz średni kwadratowy błąd ex post oraz względny błąd ex post dla prognoz wygasłych.
Wybierz metodę o najmniejszym średnim błędzie kwadratowym ex post i policz prognozę na rok 1998.
Zadanie 3
Sprzedaż benzyny na pewnej stacji benzynowej w tys. litrów w kolejnych miesiącach 2003 roku kształtowała się następująco:
41 |
38 |
39 |
40 |
39 |
42 |
38 |
39 |
41 |
42 |
40 |
39 |
Należy wyznaczyć prognozę sprzedaży benzyny na styczeń 2004 stosując następujące metody prognozowania:
- 3-elementową średnią ruchomą prostą,
- 5-elemetową średnią ruchomą prostą.
- 3-elementową średnią ruchomą ważoną (wagi: 0,2 0,3 0,5).
Kierując się średnim kwadratowym błędem ex post wybrać najbardziej trafną metodę prognozowania.
Zadanie 4 (Prosty model wygładzania wykładniczego)
Dla danych z zadania poprzedniego znaleźć prognozę na styczeń 2004 przy pomocy prostego modelu wyrównywania wykładniczego. Przyjąć stałą wygładzania α = 0,05 i α = 0,6. Wybrać tę prognozę, która jest dokładniejsza ze względu na kryterium minimalnego średniego błędu kwadratowego ex post prognoz wygasłych. Czy wybór jest taki sam, jeżeli jako kryterium zastosuje się średni względny błąd ex post prognoz wygasłych?
Zadanie 5
Ilość sprzedanego ryżu w kg w pewnym sklepie w kolejnych 10 tygodniach kształtowała się następująco:
60 |
62 |
58 |
61 |
59 |
63 |
60 |
62 |
60 |
62 |
Zbadać, czy w tym przypadku właściwe jest zastosowanie metod dla zmiennych ze stałym poziomem zmiennej prognozowanej.
Przy pomocy średniego błędu kwadratowego ex post prognoz wygasłych ocenić, która z metod daje najlepsze prognozy w tym przypadku:
- metoda naiwna
- średnia ruchoma prosta 3-elemetowa
- średnia ruchoma ważona o wagach ( 0,15 0,25 0,6 )
- proste wyrównanie wykładnicze dla α = 0,5.
Wyznaczyć prognozę sprzedaży ryżu na 11 tydzień najlepszą z tych metod.
B) Szeregi z tendencją rozwojową zmiennej prognozowanej.
Zadanie 6 (Metoda wygładzania wykładniczego Holta)
Koszty całkowite pewnej firmy usługowej w tys. zł w kolejnych kwartałach lat 2000-2002 i w trzech pierwszych kwartałach 2003 przedstawiały się następująco:
37 |
41 |
40 |
41 |
45 |
42 |
46 |
48 |
47 |
53 |
58 |
67 |
79 |
85 |
88 |
Należy wyznaczyć prognozę kosztów całkowitych tej firmy na IV kwartał 2003 roku. Zbadać dopuszczalność tej prognozy. (Przyjąć α = 0,95 β = 0,45)
Zadanie 7
Liczba ludności Polski (w mln osób) w latach 1980-1995 kształtowała się następująco:
1980 |
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
35,735 |
36,062 |
36,399 |
36,745 |
37,063 |
37,341 |
37,572 |
37,764 |
|
|
|
|
|
|
|
|
1988 |
1989 |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
37,885 |
38,038 |
38,183 |
38,309 |
38,418 |
38,505 |
38,581 |
38,609 |
Stosując model wygładzania wykładniczego Holta wyznaczyć prognozę liczby ludności na 1996 rok. Ocenić jej trafność jeżeli wiadomo, że w tym roku w Polsce było 38,639 mln mieszkańców.
(Przyjąć α = 0,9 β = 0,4)
C) Szeregi z tendencją rozwojową i z wahaniami sezonowymi zmiennej prognozowanej.
Zadanie 8 (Metoda wygładzania wykładniczego Wintersa)
Pewna firma prowadzi sprzedaż oleju opałowego. Dane dotyczące kwartalnej sprzedaży w tys. ton w latach 1999-2004 znajdują się w poniższej tabeli. Należy wyznaczyć przewidywaną wielkość sprzedaży oleju opałowego w kolejnych kwartałach 2005 roku.
(Przyjąć α = 0,5 β = 0,95 γ =0,2 )
Kwartały |
Lata |
|||||
|
1999 |
2000 |
2001 |
2002 |
2003 |
2004 |
I |
500 |
450 |
350 |
550 |
550 |
750 |
II |
350 |
350 |
200 |
350 |
400 |
500 |
III |
250 |
200 |
150 |
250 |
350 |
400 |
IV |
400 |
300 |
400 |
550 |
600 |
650 |
Zadanie 9
Liczba zawartych umów leasingowych w firmie finansowo-leasingowej w poszczególnych kwartałach lat 1996-1999 kształtowała się następująco:
20 |
10 |
4 |
11 |
33 |
17 |
9 |
18 |
45 |
23 |
14 |
11 |
25 |
60 |
30 |
13 |
Sporządzić prognozę liczby zawartych umów na kolejny rok stosując metodę Wintersa.
(Przyjąć α = 0,6 β = 0,9 γ =0,2 )
Zadanie 10
Liczba turystów odwiedzających Półwysep Helski w poszczególnych kwartałach lat 2002-2006 kształtowała się następująco:
okres |
2002kw1 |
2002kw2 |
2002kw3 |
2002kw4 |
2003kw1 |
2003kw2 |
2003kw3 |
2003kw4 |
2004kw1 |
2004kw2 |
yt |
215,1 |
371,5 |
484 |
250,1 |
228,8 |
350,9 |
506,9 |
284,7 |
282 |
436,9 |
okres |
2004kw3 |
2004kw4 |
2005kw1 |
2005kw2 |
2005kw3 |
2005kw4 |
2006kw1 |
2006kw2 |
2006kw3 |
2006kw4 |
yt |
696,7 |
466 |
468,4 |
739,8 |
921,9 |
641,9 |
770,9 |
1119,1 |
1405,2 |
892,8 |
Polecenia:
Skonstruuj wykres. Na jego podstawie określ możliwe do zastosowania metody wyznaczenia prognoz.
Zbuduj model tendencji rozwojowej. (Gretl, Microfit)
Zbuduj model tendencji rozwojowej z uwzględnieniem sezonowości.
Wyznacz prognozę na poszczególne kwartały roku 2007.
Dokonaj pełnej weryfikacji obu modeli.
Zadanie 11
Szereg czasowy kwartalnych obserwacji na PKB w Polsce w latach 2002 - 2007 przedstawia tablica:
okres |
t |
PKB |
okres |
t |
PKB |
czasu |
|
yt+1 |
czasu |
|
yt+1 |
2002.1 |
1 |
187 570,0 |
2005.1 |
13 |
229 395,80 |
2002.2 |
2 |
197 917,5 |
2005.2 |
14 |
238 094,50 |
2002.3 |
3 |
200 185,1 |
2005.3 |
15 |
241 759,80 |
2002.4 |
4 |
222 186,9 |
2005.4 |
16 |
274 052,20 |
2003.1 |
5 |
193 721,5 |
2006.1 |
17 |
242 379,20 |
2003.2 |
6 |
206 999,9 |
2006.2 |
18 |
253 924,00 |
2003.3 |
7 |
208 078,5 |
2006.3 |
19 |
261 442,60 |
2003.4 |
8 |
233 320,5 |
2006.4 |
20 |
300 109,10 |
2004.1 |
9 |
212 619,3 |
2007.1 |
21 |
267 077,20 |
2004.2 |
10 |
225 232,3 |
2007.2 |
22 |
279 582,30 |
2004.3 |
11 |
228 690,4 |
2007.3 |
23 |
|
2004.4 |
12 |
255 615,2 |
2007.4 |
24 |
|
Wyznacz prognozę na ostatnie dwa kwartały 2007 roku. Czy można wyznaczyć prognozę na pierwszy kwartał 2008 roku?
Zadanie 12
Dane kwartalne od 1Q 1997 do 2Q 2006 przedstawiono w tablicy:
EURO kurs 100 Euro w złotych,
DGD depozyty gospodarstw domowych w mln złotych,
M3 podaż pieniądza M3 w mln złotych,
BEZ stopa bezrobocia rejestrowanego (%),
PRZEWOZY przewozy ładunków w mln ton,
PRZEŁADUN przeładunki w portach w mln ton,
T trend.
Zbuduj odpowiednie modele ekonometryczne. Określ ich właściwości prognostyczne. Jeśli to możliwe skonstruuj (dobierając odpowiednią metodę) prognozę na dwa kolejne kwartały 2006 roku.
T |
EURO |
DGD |
M3 |
BEZ |
PRZEWOZY |
PRZEŁADUN |
1 |
353,15 |
86009,7 |
144931,6 |
12,6 |
88843 |
12482 |
2 |
361,65 |
92749,9 |
154747,6 |
11,6 |
99007 |
13339 |
3 |
375,36 |
99673,3 |
165037 |
10,6 |
99670 |
12250 |
4 |
355,43 |
109366,9 |
179602,4 |
10,3 |
103808 |
12914 |
5 |
381,53 |
115528,1 |
183236,3 |
10,4 |
83909 |
11286 |
6 |
378,69 |
121773 |
195388,1 |
9,6 |
93155 |
11925 |
7 |
397,53 |
129171,2 |
206639,4 |
9,6 |
101163 |
13883 |
8 |
411,24 |
138206,2 |
223913,4 |
10,4 |
98944 |
13902 |
9 |
421,44 |
147416,6 |
236748,5 |
12 |
81261 |
12170 |
10 |
418,81 |
150198,9 |
242631,2 |
11,6 |
86149 |
13159 |
11 |
416,64 |
155953,5 |
252147,9 |
12,1 |
92684 |
11845 |
12 |
434,02 |
159256,9 |
268867,8 |
13,1 |
93898 |
12505 |
13 |
406,51 |
167789,7 |
269788,1 |
14 |
79671 |
12540 |
14 |
408,44 |
177312,5 |
291886,9 |
13,6 |
85716 |
11538 |
15 |
397,74 |
182221,7 |
289140,2 |
14 |
89244 |
11861 |
16 |
391,78 |
191075,7 |
300757,3 |
15,1 |
88906 |
11932 |
17 |
377,65 |
201107,4 |
309465,8 |
16,1 |
76508 |
11683 |
18 |
363,16 |
205482,9 |
314587,3 |
15,9 |
78925 |
12783 |
19 |
367,31 |
213158,3 |
325639,6 |
16,3 |
79121 |
11399 |
20 |
366,85 |
203862,4 |
328433,8 |
17,5 |
81084 |
11889 |
21 |
362,14 |
207721,6 |
319371,8 |
18,2 |
71955 |
10910 |
22 |
366,83 |
205669,8 |
322430,2 |
17,4 |
75218 |
12265 |
23 |
380,78 |
202915,5 |
320850,2 |
17,6 |
77933 |
12000 |
24 |
385,57 |
196324,9 |
321961,2 |
18 |
79693 |
13791 |
25 |
418,45 |
195654 |
320913,5 |
18,6 |
71291 |
12146 |
26 |
426,87 |
191650,2 |
326631 |
17,7 |
79291 |
13911 |
27 |
432,1 |
190351,1 |
330893,8 |
17,5 |
82859 |
13497 |
28 |
439,78 |
195352,4 |
342943,4 |
18 |
81915 |
12256 |
29 |
477,81 |
194712,2 |
342501,3 |
20,4 |
72870 |
13380 |
30 |
473,58 |
191560,4 |
353318,2 |
19,4 |
82976 |
14271 |
31 |
463,27 |
191497,3 |
355942,3 |
18,9 |
85034 |
15299 |
32 |
453,4 |
196524,5 |
373409,1 |
19 |
84580 |
13968 |
33 |
403,03 |
201093,6 |
380227 |
19,2 |
70346 |
13473 |
34 |
408,01 |
199670,7 |
391461,3 |
18 |
78030 |
13832 |
35 |
406,08 |
199872,5 |
400989 |
17,6 |
88230 |
15915 |
36 |
402,54 |
203544 |
412346 |
17,6 |
84326 |
16259 |
37 |
383,22 |
207337,9 |
417611,9 |
17,8 |
71681 |
15008 |
38 |
394,28 |
210857,7 |
437859,5 |
16 |
87485 |
15108 |
Prognozowanie na podstawie statycznych modeli ekonometrycznych.
Zadanie 1
Dany jest oszacowany liniowy model nominalnej płacy przeciętnej w sześciu działach gospodarki (w tysiącach zł.). Na podstawie danych z przedziału m11 1990 - m3 1993:
![]()
Wt nominalna płaca przeciętna w 6-ciu działach gospodarki w tys. zł.
CPIt indeks cen w punktach %.
Dodatkowe dane:
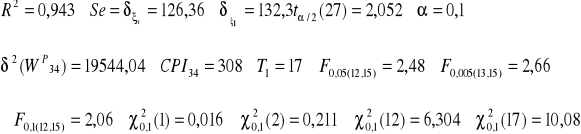
zbadaj czy model ma dobre właściwości predyktywne,
wyznacz prognozę punktową i przedziałową,
oblicz średni i względny błąd prognozy ex post,
zinterpretuj otrzymane wyniki.
Zadanie 2
Kwartalna sprzedaż środków piorących Yt w mln zł. W latach 1998-2002 opisano modelem ekonometrycznym w zależności od wydatków na reklamę (xt w tys. zł.). Otrzymano wyniki: ![]()
![]()
Wydatki na reklamę w okresach t = 18, 19, 20 wynosiły odpowiednio 10; 12; 14,5 tys. zł.
wyznacz prognozę punktową i przedziałową sprzedaży środków piorących na pierwszy kwartał 2003r,
oceń dopuszczalność powyższej prognozy, zakładając, że nie może być ona obarczona większym błędem niż 8%.
zinterpretuj wyniki.
Zadanie 3
Na podstawie danych z ośmiu lat oszacowano model:
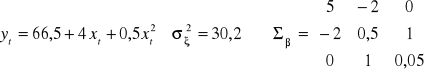
t = 1,2, ..., 8
Należy wyznaczyć prognozę punktową i przedziałową na rok 10 wiedząc, że planowana wielkość zmiennej x na ten okres będzie wynosiła 4. Przyjąć wiarygodność prognozy 0,9 (![]()
).
Zadanie 4
Oszacowano model liniowy:
gdzie: x- dochód w mln zł.,
c- cena w tys. zł/kg,
p- popyt w kg.
Wyniki oszacowań przedstawiają się następująco:
![]()
![]()
![]()
Zinterpretuj postać liniową modelu uwzględniając średnie błędy szacunku.
Oblicz i zinterpretuj prognozę zmiennej objaśnianej wiedząc, że , natomiast średni błąd prognozy wynosi 2,5.
Oblicz i zinterpretuj elastyczności cenowe i dochodowe w punkcie prognozy.
Zadanie 5
Na podstawie statycznego liniowego modelu wydatków gospodarstw domowych na energię (oszacowanego w oparciu o próbę czasową) wyznaczono ich prognozę z wyprzedzeniem jednookresowym: 0,2 mln zł na osobę miesięcznie. Względny błąd prognozy wyniósł 4.5%. Zapisz i zinterpretuj przedział ufności dla wydatków w okresie prognozowanym, przyjmując ![]()
=2.01 dla =0.05.
Zadanie 6
Na podstawie próby obejmującej lata 1990-1999 oszacowano parametry funkcji uzależniającej sprzedaż energii elektrycznej (mln MWh) od długości linii przesyłowych (w tys. km) i liczby odbiorców (tys), otrzymując następujące oszacowanie:
gdzie: E - sprzedaż energii, D - długość linii przesyłowych, L - liczba odbiorców.
Wiadomo ponadto, że macierz wariancji i kowariancji estymatorów parametrów strukturalnych jest następująca:
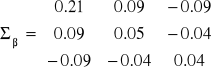
oraz: 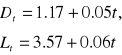
,
t=1,2,...,10, ![]()
.
Wyznacz prognozę sprzedaży energii na rok 2002 (punktową i przedziałową), czy prognoza jest dopuszczalna, jeśli maksymalny względny błąd prognozy wynosi 5%?
Zadanie 7
Na podstawie 60 obserwacji z okresu 1996M1- 2000M12, gdzie:
Y - produkcja energii w elektrowniach wodnych w województwie Pomorskim (w kWh.),
X1 - przepływ wody w elektrowniach (w mln m3),
X2 - czas przestoju elektrowni (w godz.),
oszacowany został następujący model ekonometryczny:
![]()
RSK = 1 680 000.
![]()
Następnie szereg obserwacji podzielony został na dwie części: od 1996M1 do 1997M12 oraz od 1998M1 do 2000M12. Oszacowane zostały oddzielne modele dla obu podrób:
(1) ![]()
RSK = 80 400.
![]()
(2) ![]()
RSK = 1 580 000.
![]()
Stosując odpowiedni test stabilności parametrów strukturalnych modelu, należy ocenić właściwości predyktywne modelu.
Zadanie 8
Oszacowano model sprzedaży produktów firmy Alka-Selther, gdzie, y - wartość sprzedaży firmy w tys. $, x1 - wydatki na reklamy w radio i telewizji w tys. $, x2 - wydatki na pokazy w sklepach tys. $. Dla 10 obserwacji wyniki oszacowania modelu przedstawiają się następująco:
![]()
Ponadto wiadomo, że: RSK = 25,5619 oraz ![]()
.
Szereg 10 obserwacji podzielono na dwie równe podpróby: t1 = 5 i t2 = 5. Uzyskano następujące oszacowanie obu modeli:
(1) ![]()
RSK = 0,2194 oraz ![]()
;
(2) ![]()
RSK = 17,0826 oraz ![]()
.
1
5
Wyszukiwarka
Podobne podstrony:
Interpretacje do zadania 1, UE Katowice, Gospodarka Turystyczna Mgr I rok, prognozowanie cwiczenia,
ZADANIA Z ĆWICZEŃ(1)
kryteria do zadania cwiczeniowego
Zadaniedo8 ćwiczenia KORELACJA, Rok I, matematyka
psio zadania cwiczenia-1, Programowanie
Zadania - ćwiczenia, Fizyka - zestaw zadań, Fizyka
Zadania ćwiczenia 9
Ćwiczenie 5 przykład, osmoza
Cel i zadania ćwiczeń oddechowych
GW Cwiczenie02 przyklad
Java Zadania z programowania z przykładowymi rozwiązaniami
zadania z ćwiczeń, 2, Zad
Przykładowe zadania praktyczne, Przykładowe Zadanie - Opracował Anklewicz, Propozycja zadania egzami
Przykładowe zadania praktyczne, Przykładowe Zadanie - Opracował Wiertelczyk, Przykład zadania prakty
Zadania - ćwiczenia, ciepło, Zadania
zadania z ćwiczeń, stata2, 1)Wariancja skosnosci ma zawsze wartosc dodatna - NIE
zadania z ćwiczeń, 1.1, 1
zadania z ćwiczeń, stata2, 1)Wariancja skosnosci ma zawsze wartosc dodatna - NIE
zadania z ćwiczeń, 1.1, 1
więcej podobnych podstron