Numer ćwiczenia 3	Temat ćwiczenia Rezonans akustyczny	Ocena z teorii
Numer zespołu	Nazwisko i imię Witkowicz Jakub	Ocena zaliczenia ćwiczenia
Data 6.04.2004	Wydział, rok, grupa EAIiE rok Ib gr. VII	Uwagi

Cel ćwiczenia:

Obserwacja powstania rezonansu fal akustycznych w rurze Quinckego, pomiar prędkości dźwięku w różnych gazach oraz wyznaczenie stosunku c_p/c_v i liczby stopni swobody molekuł gazu.

Wprowadzenie teoretyczne

Falą nazywamy zjawisko rozchodzenia się drgań. Fale powstające w ośrodku sprężystym nazywamy falami mechanicznymi. Fale mechaniczne możemy podzielić na poprzeczne i podłużne.

Fale dźwiękowe - są to podłużne, mechaniczne fale rozchodzące się w różnych ośrodkach np. w ciałach stałych, cieczach i gazach. Ucho ludzkie potrafi usłyszeć dźwięki z zakresu częstotliwości 20-20000 Hz. Fale o częstotliwościach niższych od 20Hz nazywamy infradźwiękami (podźwiękami), natomiast fale o częstotliwościach większych od 20kHz nazywamy ultradźwiękami (naddźwiękami).

Fala dźwiękowa rozchodząca się w rurze, wytwarzana przez głośnik jest falą biegnącą opisaną wzorem:

y = y_m sin(ωt-kx) , gdzie y_m - wychylenie maksymalne.

, gdzie λ - długość fali

, gdzie, ω - czestość fali, T - okres

Zjawisko interferencji (nakładania się fal), zgodnie z tzw. zasadą superpozycji fal, amplituda fali wypadkowej w każdym punkcie dana jest wzorem:

gdzie: A₁, A₂ - amplitudy fal cząstkowych, φ - różnica faz obu fal.

Maksymalnie A = A₁+A₂ dla φ=2k (fazy zgodne), minimalnie A=A₁-A₂ dla φ=(2k+1) (fazy przeciwne). Warunkiem zaistnienia stałego w czasie rozkładu przestrzennego amplitudy interferujących fal jest ich spójność (koherentność).Wypadkowa fala, powstała z interferencji spójnych fal padających jest falą stojącą. Fala podłużna ma kierunek propagacji fali, natomiast fala poprzeczna ma przemieszczenie skierowane prostopadle do kierunku propagacji.

Prędkość rozchodzenia się fali podłużnej w ciele stałym jest równa:

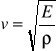
, gdzie E - moduł Younga, ρ - gęstość ciała

Prawie identyczną postać wzoru otrzymujemy dla cieczy lub gazu:

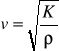
, gdzie K= Δp /(ΔV/V) - moduł sprężystości objętościowej, ρ - gęstość ośrodka drgającego

Prędkość rozchodzenia się fali poprzecznej w ciele stałym jest równa:

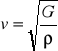
, gdzie G - moduł sprężystości

Zwykle w danym ciele fala podłużna rozchodzi się szybciej niż fala poprzeczna, stąd moduł Younga jest większy od modułu sprężystości.

Przyjmujemy, że rozchodzenie się dźwięku w powietrzu jest procesem adiabatycznym oraz, że

, gdzie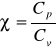

W warunkach normalnych większość gazów wykazuje własności bardzo zbliżone do gazu doskonałego.

i dzieląc stronami dwa ostatnie równania:

zatem prędkość rozchodzenia się fali wynosi:

gdzie

   to prędkość dźwięku w temperaturze T_o =  273K (0^oC)

więc, podstawiając to do równania na prędkość dźwięku otrzymujemy:

gdzie T - temperatura bezwzględna, R - uniwersalna stała gazowa, μ - masa molowa cząsteczki gazu,

R= 8,31 J/(K mol).

Pokazuje to wyraźnie, że prędkość dźwięku nie zależy od ciśnienia. Ponieważ dla danej masy gazu jego skład i temperatura są znane. Wzór ten umożliwia obliczenie κ. Z kolei ta wartość zależy od ilości stopni swobody i molekuły gazu:

Stopień swobody jest to zespół niezależnych zmiennych koniecznych wystarczających do opisania stanu układu fizycznego w każdej chwili czasowej. Liczbę stopni swobody „i” można wyznaczyć z zależności :

3. Wyniki pomiarów

Lp.	f [Hz]	1/f [Hz]	Położenie słupa wody w rezonansie λ/2 [m]	λśr/2 [m]	λśr/2 [m]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

---