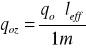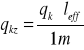Wymiary żebra: -szerokość -wysokość -grubość płyty

Beton klasy B-37

Stal klasy

III. Obliczenia żebra:

III.1. Schemat statyczny żebra:

b) wymiary żebra:

b = 20 [cm]

h = 40 [cm]

III.2 Zestawienie obciążeń:

OBCIĄŻENIE	Wartości Charakter/ Obliczeniowe [kN/m]
Obciążenie stałe: -obliczeniowe: -charakterystyczne: go=3,13 [kN/m^2] współczynnik obciążenia ciężar objętościowy betonu goż =3,13*2,40+(0,40-0,08)*0,20*27*1,1=9,41 [kN/m] gk=2,77[kN/m^2] gkż=2,77*2,40+(0,40-0,08)*0,20*27=8,38 [kN/m]	goż=9,41 gkż=8,38
Obciążenie zmienne: -obliczeniowe: -charakterystyczne: qo=6,971 [kN/m^2] qoż=6,971*2,40=16,73 [kN/m] qk=5,61[kN/m^2] qkż=5,61*2,40=13,464[kN/m]	qoż=16,73 qkż=13,46
RAZEM OBCIĄŻENIA CAŁKOWITE na 1 mb projektowanego żebra	POż=26,14

Obciążenia całkowite na 1 mb żebra:

1. obliczeniowe:

p_oż = g_o + q_o = 9,41 +16,73 = 26,14 [kN/m]

2. charakterystyczne:

p_kż = g_k + q_k = 21,84 [kN/m]

III.3. Obliczenia statyczne:

III.3.1. Wyznaczenie obwiedni momentów oraz obwiedni sił tnących od obciążeń obliczeniowych (Metoda plastycznego wyrównania momentów):

l_n1=5,8-0,20-0,10=5,5 [m]

l_n2=5,8-0,20=5,6 [m]

1. Momenty przęsłowe:

- w prześle skrajnym:

- w przęsłach pośrednich:

2. Momenty podporowe:

- podpora A (moment utwierdzenia):

* zasięg momentu w utwierdzeniu:

= 0,15 ·5,5 = 0,82 [kNm]

- podpora B,E

M_B= M_E

- podpora C, D,

M_c = M_D=

3. Momenty ujemne w przęsłach:

Zakłada się że przęsła obciążone są obciążeniem zastępczym o wartości:

M_przęsł. =

M_przęsł.^AB =

M_przęsł.^BC = M_przęsl^DE=

M_przęsł.^CD =

Obwiednia momentów wyznaczona metodą plastycznego wyrównania momentów:

Wyznaczenie obwiedni sił tnących żebra.

Obliczenia sił tnących żebra:

Obwiednia sił tnących dla żebra:

III.3.2. Metoda liniowo sprężysta, obliczenia wykorzystaniem tablic Winklera: (obciążenia obliczeniowe):

Maksymalne i minimalne momenty przęsłowe oraz momenty podporowe:

M _{max AB} = α_g*g_oż*l^2 + α_qmax *q_oż*l^2 [kNm]

M _{min AB} = α_g*g_oż*l^2 + α_qmin *q_oż*l^2 [kNm]

M_utw = 0,25 M_maxAB [kNm]

Zestawienie wyników obliczeń:

goż [kN/m]=	9,41
qoż [kN/m]=	16,73

	[kNm]	alfa g	alfa q	l [m]
M a=	20,2506
M ab max=	81,0025	0,0781	0,1	5,80
M ab min=	9,92118	0,0781	-0,0263	5,80
M bc max=	54,77	0,0331	0,0787	5,80
M bc min=	-15,4108	0,0331	-0,046	5,80
M cd max=	62,7439	0,0462	0,0855	5,80
M cd min=	-7,60577	0,0462	-0,0395	5,80
M b max=	-100,211	-0,105	-0,119	5,80
M b min=	-25,9216	-0,105	0,013	5,80
M c max=	-87,4781	-0,079	-0,111	5,80
M c min=	-14,8773	-0,079	0,018	5,80

Obwiednia momentów wyznaczona metodą liniowo sprężystą:

Siły poprzeczne i reakcje:

R_A = α_g * g_oż *l+ α_qmax * q_oż *l [kN]

T a=	64,9604	0,3948	0,4474	5,80
T bl=	-93,1808	-0,605	-0,62	5,80
T bp=	86,7604	0,5263	0,5981	5,80
T cl=	-81,8034	-0,4737	-0,5766	5,80
T cp=	84,6264	0,5	0,5909	5,80

Obwiednia sił tnących dla żebra wyznaczona metoda liniowo sprężystą:

3. Metoda liniowo sprężysta, obliczenia wykorzystaniem tablic winklera: (obciążenia charakterystyczne):

gkż [kN/m]=	8,38
qkż [kN/m]=	13,46

	[kNm]	alfa g	alfa q	l [m]
M a=	16,824
M ab max=	67,296	0,0781	0,1	5,80
M ab min=	10,108	0,0781	-0,0263	5,80
M bc max=	44,966	0,0331	0,0787	5,80
M bc min=	-11,498	0,0331	-0,046	5,80
M cd max=	51,738	0,0462	0,0855	5,80
M cd min=	-4,8615	0,0462	-0,0395	5,80
M b max=	-83,482	-0,105	-0,119	5,80
M b min=	-23,714	-0,105	0,013	5,80
M c max=	-72,531	-0,079	-0,111	5,80
M c min=	-14,12	-0,079	0,018	5,80

Siły poprzeczne i reakcje:

T a=	54,116	0,3948	0,4474	5,80
T bl=	-77,786	-0,6052	-0,6196	5,80
T bp=	72,273	0,5263	0,5981	5,80
T cl=	-68,038	-0,4737	-0,5766	5,80
T cp=	70,432	0,5	0,5909	5,80

III.4.Stopień zbrojenia:

Minimalny stopień zbrojenia:

Zgodnie z pkt. 4.8, PN-B03264:2002:

Maksymalny stopień zbrojenia:

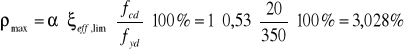
gdzie: A_s,min - minimalny przekrój zbrojenia;

- minimalny, maksymalny stopień zbrojenia;

α - współczynnik redukujący wytrzymałość;

f_cd­ - wytrzymałość obliczeniowa betonu;

f_yd - wytrzymałość obliczeniowa stali;

d - wysokość użyteczna przekroju;

b - szerokość przekroju

Wysokość użytkowa:

Wysokość użytkowa z uwzględnieniem skosu ukrytego:

gdzie: φ_g - średnica prętów zbrojenia głównego,

przyjęto:
;

φ_s - średnica prętów zbrojenia strzemion,

przyjęto:
;

c - grubość otulenia,

;

c_min - minimalna grubość otulenia

przyjęto: c_min =10 [mm] (tab.21 PN-B-03264:2002);

Δh - odchyłka wymiarowa,

III.5.Dobór przekroju zbrojenia:

Podpora A

Obliczanie przekroju zbrojenia:

W celu doboru zbrojenia na podporach sprawdzamy dwa przypadki:

1) dla momentu licowego;

2) dla momentu osiowego ale z uwzględnieniem skosu ukrytego.

1)

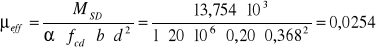
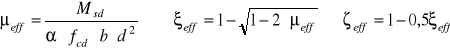
ξ_eff = 0,0257 ζ_eff = 0,987

ξ_eff < ξ_eff,lim ξ_eff,lim = 0,53 0,0257 < 0,53

Wymagany przekrój zbrojenia:

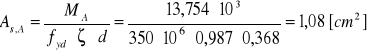
M_sd - wartość momentu obciążającego dany przekrój;

α - współczynnik redukujący wytrzymałość;

f_cd­ - wytrzymałość obliczeniowa betonu;

f_yd - wytrzymałość obliczeniowa stali;

d - wysokość użyteczna przekroju;

b - szerokość przekroju (b = 0,2 m).

- współczynniki

Minimalny przekrój zbrojenia:

[cm²]

Warunek spełniony - do dalszych obliczeń As₁=1,08 [cm²].

2)

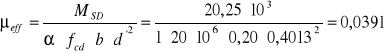
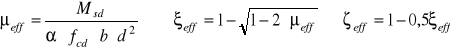
ξ_eff = 0,0398 ζ_eff = 0,98

ξ_eff < ξ_eff,lim ξ_eff,lim = 0,53 0,0398< 0,53

Wymagany przekrój zbrojenia:

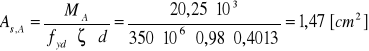
Minimalny przekrój zbrojenia:

[cm²]

Warunek spełniony- do dalszych obliczeń As₁=1,47 [cm²]

Do dalszych obliczeń przyjmuje wartość A= 1,47[cm²].

Przęsło AB

Określenie rodzaju przekroju:

przekrój pozornie teowy.

Z przeprowadzonych obliczeń wynika, że w przęśle AB występuje przekrój pozornie teowy, co oznacza, że oś obojętna przechodzi przez płytę. W takim wypadku przekrój ten traktujemy w obliczeniach jak zwykłą belkę o przekroju prostokątnym.

Obliczanie przekroju zbrojenia:

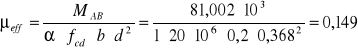
ξ_eff = 0,162 ζ_eff = 0,919

ξ_eff < ξ_eff,lim ξ_eff,lim = 0,53 0,162 < 0,53

Wymagany przekrój zbrojenia:

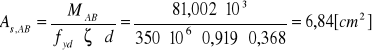
Warunek spełniony do dalszych obliczeń przyjmuje wartość AB= 6,84 [cm²].

Podpora B

Obliczanie przekroju zbrojenia:

W celu doboru zbrojenia na podporach sprawdzam dwa przypadki:

1) dla momentu licowego,

2) dla momentu osiowego ale z uwzględnieniem skosu ukrytego.

1)

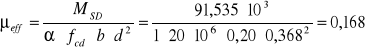
ξ_eff = 0,185 ζ_eff =0,907

ξ_eff < ξ_eff,lim ξ_eff,lim = 0,53 0,185< 0,53

Wymagany przekrój zbrojenia:

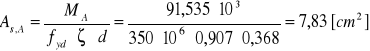
Minimalny przekrój zbrojenia:

[cm²]

- warunek spełniony.

2)

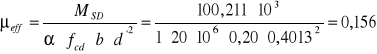
ξ_eff = 0,17 ζ_eff = 0,915

ξ_eff < ξ_eff,lim ξ_eff,lim = 0,53 0,17< 0,53

Wymagany przekrój zbrojenia:

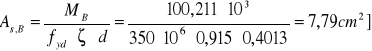
Do dalszych obliczeń przyjmuje wartość B= 7,83[cm²].

Przęsło BC

1) moment dodatni:

Określenie rodzaju przekroju:

przekrój pozornie teowy

Oś obojętna przechodzi przez płytę.

Obliczanie przekroju zbrojenia:

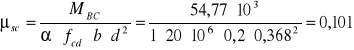
ξ_eff = 0,107 ζ = 0,946

ξ_eff < ξ_eff,lim ξ_eff,lim = 0,53 0,107< 0,53

Wymagany przekrój zbrojenia:

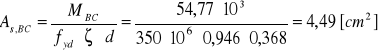
- warunek spełniony

Do dalszych obliczeń przyjmuje wartość przekroju zbrojenia dla momentu dodatniego BC⁺ = 4,49 [cm²]

2) moment ujemny:

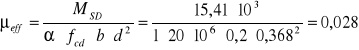
ξ_eff = 0,0284 ζ_eff=0,986

ξ_eff < ξ_eff,lim ξ_eff,lim = 0,53 0,0284 < 0,53

Wymagany przekrój zbrojenia:

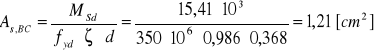
Minimalny przekrój zbrojenia:

[cm²]

- warunek jest spełniony.

Do dalszych obliczeń przyjmuje wartość przekroju zbrojenia dla momentu ujemnego BC^- = 1,21[cm²]

Podpora C

Obliczanie przekroju zbrojenia:

W celu doboru zbrojenia na podporach sprawdzam dwa przypadki:

1) dla momentu licowego,

2) dla momentu osiowego ale z uwzględnieniem skosu ukrytego.

1)

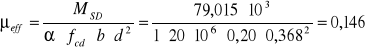
ξ_eff = 0,158 ζ_eff =0,921

ξ_eff < ξ_eff,lim ξ_eff,lim = 0,53 0,158< 0,53

Wymagany przekrój zbrojenia:

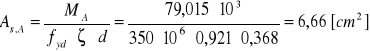
Minimalny przekrój zbrojenia:

[cm²]

- warunek spełniony.

2)

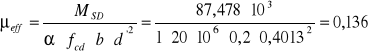
ξ_eff = 0,146 ζ_eff = 0,927

ξ_eff < ξ_eff,lim ξ_eff,lim = 0,53 0,146 < 0,53

Wymagany przekrój zbrojenia:

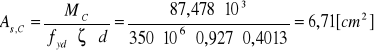
Do dalszych obliczeń przyjmuje wartość C=6,71[cm²].

Przęsło CD

1) moment dodatni:

Określenie rodzaju przekroju:

przekrój pozornie teowy

Oś obojętna przechodzi przez płytę.

Obliczanie przekroju zbrojenia:

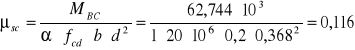
ξ_eff = 0,123 ζ = 0,938

ξ_eff < ξ_eff,lim ξ_eff,lim = 0,53 0,123< 0,53

Wymagany przekrój zbrojenia:

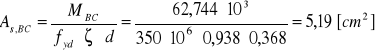
- warunek spełniony.

Do dalszych obliczeń przyjmuje wartość przekroju zbrojenia dla momentu dodatniego CD⁺ = 5,19 [cm²].

2) moment ujemny:

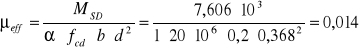
ξ_eff = 0,0141 ζ_eff=0,993

ξ_eff < ξ_eff,lim ξ_eff,lim = 0,53 0,0141 < 0,53

Wymagany przekrój zbrojenia:

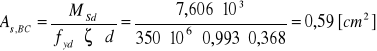
Minimalny przekrój zbrojenia:

[cm²]

- warunek nie jest spełniony.

Do dalszych obliczeń przyjmuje wartość przekroju zbrojenia dla momentu ujemnego BC^- = 0,956[cm²]

Zestawienie przekrojów zbrojenia dla żebra:

ELEMENT	MOMENT OBCIĄŻAJĄCY	WYMAGANE POLE POW.ZBROJENIA	MINIMALNE POLE POW.ZBROJENIA	DOBRANE ZBROJENIE A [cm^2]	RZECZYWISTE POLE POW.ZBROJENIA A [cm^2]
		M [kNm]	A [cm^2]			A [cm^2]
Podpora A	20,25	1,47	1,04	2x Φ12 mm	2,26
Przęsło AB(dołem)	81,002	6,84	0,956	4x Φ 15 mm	7,07
Podpora B	100,211	7,83	0,956	4x Φ 16 mm	8,04
Przęsło BC(górą)	15,41	1,21	0,956	1x Φ 14 mm	1,54
Przęsło BC(dołem)	54,77	4,49	0,956	3x Φ 14 mm	4,62
Podpora C	87,478	6,71	0,956	4x Φ 15 mm	7,07
Przęsło CD(górą)	7,606	0,956	0,956	1x Φ 12 mm	1,13
Przęsło CD(dołem)	62,744	5,19	0,956	3xΦ15 mm	5,30

III.6.Wymiarowanie żebra na ścinanie:

f_{ctd =} 1,33 [MPa]=1,33·10⁶[Pa]= 1,33·10³[kN/m]

f_{cd =} 20[MPa]=20·10⁶[Pa]= 20·10³[kN/m]

f_{ck =} 30 [MPa]=30·10⁶[Pa]=30·10³[kN/m]

f_{ydw1 =} 190 [MPa]=190·10⁶[Pa]= 190·10³[kN/m]

f_yk= 220 [MPa]=220·10⁶[Pa]= 220·10³[kN/m]

• cotθ=1

• A_sw1=2·π·0,04²=1,005·10^-4[m²] - strzemiona dwu cięte o średnicy 8 [mm]

• współczynnik efektywności:
  

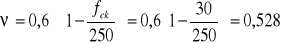
• k - współczynnik,

- do podpory doprowadzono 50% rozciąganego zbrojenia przęsłowego;

• b_w=0,20[m]

• z = 0,9·d = 0,331 [m]

1. Przy podporze A:

Siła poprzeczna na krawędzi podpory skrajnej V_sd wywołana obciążeniem obliczeniowym.

Sprawdzenie nośności na ścinanie w elemencie nie posiadającym zbrojenia.

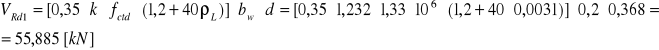
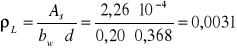
⇒wymagane zbrojenie na ścinanie

Nośność odcinków drugiego rodzaju.

Zakłada się zbrojenie na ścinanie złożone ze strzemion prostopadłych .

Sprawdzenie nośności krzyżulców betonowych:

- odcinek II rodzaju

Rozstaw strzemion;

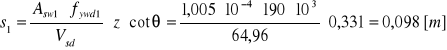
Strzemiona: 4 strzemiona φ8 co 9 cm .

2. Przy podporze B (z prawej strony)

Sprawdzenie nośności na ścinanie w elemencie nie posiadającym zbrojenia.

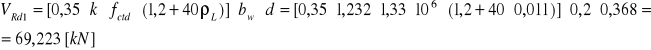
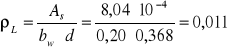
⇒wymagane zbrojenie na ścinanie

Nośność odcinków drugiego rodzaju.

Zakłada się zbrojenie na ścinanie złożone ze strzemion prostopadłych.

Sprawdzenie nośności krzyżulców betonowych:

Rozstaw strzemion

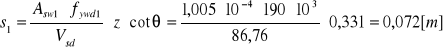
Strzemiona: 10 strzemion φ8 co 7 cm.

3. Przy podporze B (z lewej strony)

Sprawdzenie nośności na ścinanie w elemencie nie posiadającym zbrojenia.

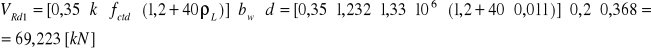
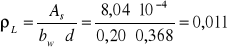
⇒wymagane zbrojenie na ścinanie

Nośność odcinków drugiego rodzaju.

Zakłada się zbrojenie na ścinanie złożone ze strzemion prostopadłych.

Sprawdzenie nośności krzyżulców betonowych:

Rozstaw strzemion:

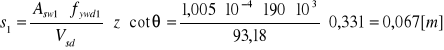
Strzemiona: 16 strzemion φ8 co 6 cm.

4. Przy podporze C (z prawej strony)

Sprawdzenie nośności na ścinanie w elemencie nie posiadającym zbrojenia.

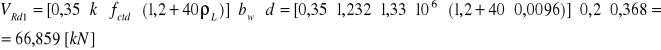
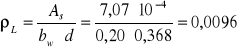
⇒wymagane zbrojenie na ścinanie

Nośność odcinków drugiego rodzaju.

Zakłada się zbrojenie na ścinanie złożone ze strzemion prostopadłych

Sprawdzenie nośności krzyżulców betonowych:

Rozstaw strzemion:

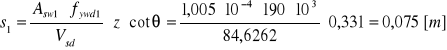
Strzemiona: 10 strzemion φ8 co 7 cm.

5. Przy podporze C (z lewej strony)

Sprawdzenie nośności na ścinanie w elemencie nie posiadającym zbrojenia.

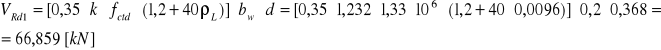
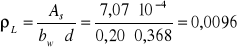
⇒wymagane zbrojenie na ścinanie

Nośność odcinków drugiego rodzaju.

Zakłada się zbrojenie na ścinanie złożone ze strzemion prostopadłych

Sprawdzenie nośności krzyżulców betonowych:

Rozstaw strzemion

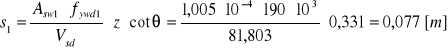
Strzemiona: 9 strzemion φ8 co 7 cm.

III.7.Sprawdzenie stanów granicznych nośności:

Sprawdzenie stanu nośności na zarysowanie polega na wykazaniu że występujące siły wewnętrzne wyznaczone dla kombinacji obciążeń długotrwałych nie powodują rozwarcia rys prostopadłych do osi elementu większych nad szerokości uznanych za graniczne.

III.7.1. Sprawdzenie stanu granicznego zarysowanie:

WgPN-B-03264 graniczna szerokość rys dla konstrukcji żelbetowych klasy ekspozycji X0 wynosi: w_lim=0,3 mm .

III.7.2. Szerokość rozwarcia rys prostopadłych do osi elementu:

Przęsło AB:

Do obliczeń przyjmuje się przekrój o wymiarach bxh (0,2 x 0,4)m

W_k=β·S_rm·ε_sm

W_k -obliczeniowa szerokość rys prostopadłych do osi elementu

β=1,3 -dla przekrojów których najmniejszy wymiar nie przekracza 300 mm

• średni końcowy rozstaw rys:

=50+0,25·1,6·0,5·(15/0,0442)=117,87mm

gdzie: k₁=1,6 dla prętów gładkich (współczynnik zależny od przyczepności prętów)

k₂=0,5 w przypadku rozkładu trójkątnego jak przy zginaniu (współczynnik zależny od rozkładu odkształceń w strefie rozciąganej)

Φ=15 mm średnica prętów rozciąganych

β₁=0,5 dla prętów gładkich (współczynnik zależny od przyczepności prętów)

β₂=0,5 dla obciążenia długotrwałego (współczynnik zależny od czasu działania i powtarzalności obciążenia)

ρ_r =
=
=0,0442 -efektywny stopień zbrojenia

=2,5(0,40-0,368)0,2=160 cm²

• średnia różnica odkształcenia zbrojenia rozciąganego w betonie:

ε_sm=
12,54·10^-4

• naprężenia w zbrojeniu (w stanie zarysowania):

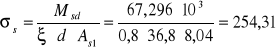
MPa

• rzeczywisty stopień zbrojenia w przęśle AB:

ρ_s =

=1,09%

przyjmuję ξ=0,8; według załącznika D do normy PN-B-03264 dla ρ>1%

• -moment zginający od obciążeń charakterystycznych wg metody liniowo sprężystej w przęśle skrajnym:

67,296kNm

• -moment rysujący:

=f_ctm·W_c=2900 · 0,00533 = 15,457kNm

• -wskaźnik wytrzymałości przekroju:

W_c=
[m³]

• szerokość rozwarcia rys prostopadłych do osi elementu wynosi:

W_k=β·S_rm·ε_sm=1,3·117,87 ·12,54·10^-4=0,192 [mm]

W_k=0,192< W_lim=0,3mm (warunek spełniony).

Stan graniczny rozwarcia rys prostopadłych do elementu nie został przekroczony.

Przęsło BC:

W_k=β·S_rm·ε_sm

W_k -obliczeniowa szerokość rys prostopadłych do osi elementu

β=1,3 -dla przekrojów których najmniejszy wymiar nie przekracza 300 mm

• średni końcowy rozstaw rys:

=50+0,25·1,6·0,5·(14/0,0289)=136,886 mm

gdzie: k₁=1,6 dla prętów gładkich (współczynnik zależny od przyczepności prętów)

k₂=0,5 w przypadku rozkładu trójkątnego jak przy zginaniu (współczynnik zależny od rozkładu odkształceń w strefie rozciąganej)

Φ=14 mm średnica prętów rozciąganych

β₁=0,5 dla prętów gładkich (współczynnik zależny od przyczepności prętów)

β₂=0,5 dla obciążenia długotrwałego (współczynnik zależny od czasu działania i powtarzalności obciążenia)

ρ_r =
=
=0,0289 -efektywny stopień zbrojenia

=2,5(0,40-0,368)0,2=160 cm²

• średnia różnica odkształcenia zbrojenia rozciąganego w betonie:

ε_sm=
14,46·10^-4

• naprężenia w zbrojeniu (w stanie zarysowania):

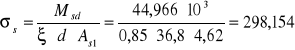
MPa

• rzeczywisty stopień zbrojenia w przęśle BC:

ρ_s =

=0,63%

przyjmuję ξ=0,85; według załącznika D do normy PN-B-03264 dla 0,5%<ρ>1%

• -moment zginający od obciążeń charakterystycznych w przęśle skrajnym:

44,966 kNm

• -moment rysujący:

=f_ctm·W_c=2900 · 0,00533 = 15,457 kNm

• -wskaźnik wytrzymałości przekroju:

W_c=
[m³]

• szerokość rozwarcia rys prostopadłych do osi elementu wynosi:

W_k=β·S_rm·ε_sm=1,3·136,886·14,46·10^-4=0,257 [mm]

W_k=0,257< W_lim=0,3mm (warunek spełniony).

Stan graniczny rozwarcia rys prostopadłych do elementu nie został przekroczony.

Przęsło CD:

W_k=β·S_rm·ε_sm

W_k -obliczeniowa szerokość rys prostopadłych do osi elementu

β=1,3 -dla przekrojów których najmniejszy wymiar nie przekracza 300 mm

• średni końcowy rozstaw rys:

=50+0,25·1,6·0,5·(15/0,0331)=138,634mm

gdzie: k₁=1,6 dla prętów gładkich (współczynnik zależny od przyczepności prętów)

k₂=0,5 w przypadku rozkładu trójkątnego jak przy zginaniu (współczynnik zależny od rozkładu odkształceń w strefie rozciąganej)

Φ=15 mm średnica prętów rozciąganych

β₁=0,5 dla prętów gładkich (współczynnik zależny od przyczepności prętów)

β₂=0,5 dla obciążenia długotrwałego (współczynnik zależny od czasu działania i powtarzalności obciążenia)

ρ_r =
=
=0,0331 -efektywny stopień zbrojenia

=2,5(0,40-0,368)0,2=160 cm²

• średnia różnica odkształcenia zbrojenia rozciąganego w betonie:

ε_sm=
15,17·10^-4

• naprężenia w zbrojeniu (w stanie zarysowania):

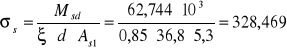
MPa

• rzeczywisty stopień zbrojenia w przęśle BC:

ρ_s =

=0,72%

przyjmuję ξ=0,85; według załącznika D do normy PN-B-03264 dla 0,5%<ρ>1%

• -moment zginający od obciążeń charakterystycznych w przęśle skrajnym:

62,744kNm

• -moment rysujący:

=f_ctm·W_c=2900 · 0,00533 = 15,457 kNm

• -wskaźnik wytrzymałości przekroju:

W_c=
[m³]

• szerokość rozwarcia rys prostopadłych do osi elementu wynosi:

W_k=β·S_rm·ε_sm=1,3·138,634 ·15,17·10^-4=0,273 [mm]

W_k=0,273< W_lim=0,3mm (warunek spełniony)

Stan graniczny rozwarcia rys prostopadłych do elementu nie został przekroczony.

III.7.3. Szerokość rozwarcia rys ukośnych:

• szerokość rys ukośnych W_k wynosi:

W_k=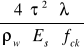
[mm]

Dla strefy przy podporze A

• naprężenie ścinające w strefie przypodporowej:

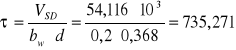
[kPa]

• stopień zbrojenia strzemionami prostopadłymi do osi elementu:

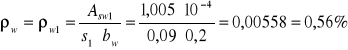
• wartość λ oblicza się ze wzoru:

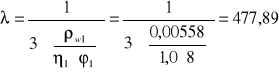
φ₁- średnica strzemion pionowych w mm, 8[mm]

η₁- współczynnik zależny od przyczepności strzemion pionowych; 1,0 dla prętów gładkich

W_k=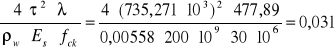
[mm]

Dla strefy przy podporze B(z prawej strony)

• naprężenie ścinające w strefie przypodporowej:

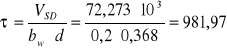
[kPa]

• stopień zbrojenia strzemionami prostopadłymi do osi elementu:

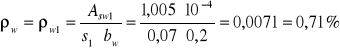
• wartość λ oblicza się ze wzoru:

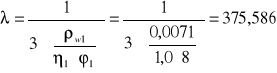
φ₁- średnica strzemion pionowych w mm; 8[mm]

η₁- współczynnik zależny od przyczepności strzemion pionowych, 1,0 dla prętów gładkich

W_k=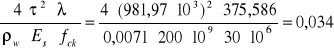
[mm]

Dla strefy przy podporze B(z lewej strony)

• naprężenie ścinające w strefie przypodporowej:

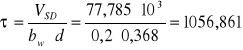
[kPa]

• stopień zbrojenia strzemionami prostopadłymi do osi elementu:

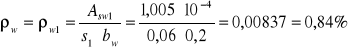
• wartość λ oblicza się ze wzoru:

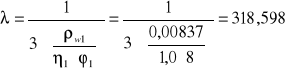
φ₁- średnica strzemion pionowych w mm, 8[mm]

η₁- współczynnik zależny od przyczepności strzemion pionowych, 1,0 dla prętów gładkich

W_k=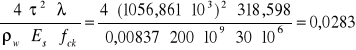
[mm]

Dla strefy przy podporze C ( z prawej strony)

• naprężenie ścinające w strefie przypodporowej:

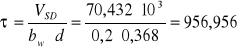
[kPa]

• stopień zbrojenia strzemionami prostopadłymi do osi elementu:

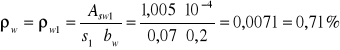
• wartość λ oblicza się ze wzoru:

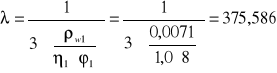
φ₁- średnica strzemion pionowych w mm, 8[mm]

η₁- współczynnik zależny od przyczepności strzemion pionowych, 1,0 dla prętów gładkich

W_k=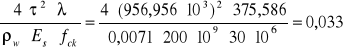
[mm]

Dla strefy przy podporze C ( z lewej strony)

• naprężenie ścinające w strefie przypodporowej:

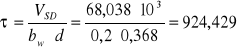
[kPa]

• stopień zbrojenia strzemionami prostopadłymi do osi elementu:

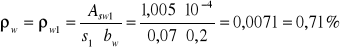
• wartość λ oblicza się ze wzoru:

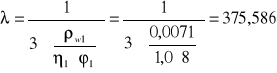
φ₁- średnica strzemion pionowych w mm, 8[mm]

η₁- współczynnik zależny od przyczepności strzemion pionowych, 1,0 dla prętów gładkich

W_k=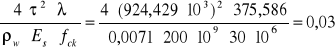
[mm]

Stan graniczny zarysowanie dla wystąpienia rys ukośnych nie został przekroczony w żadnej strefie przypodporowej.

III.7.4. Sprawdzenie stanu granicznego ugięcia:

Sprawdzenie stanu granicznego ugięć polega na wyznaczeniu, ze występujące w konstrukcji siły wewnętrzne wyznaczone dla kombinacji obciążeniem długotrwałym nie powodują ugięć większych od uznanych za graniczne ze względu na przeznaczenie budowli, możliwości uszkodzenia przylegających elementów nie konstrukcyjnych, odczucia estetyczne użytkowników.

Przęsło AB:

W przypadku gdy: l_eff < 6,0 [m]

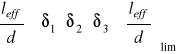
• Wskaźnik sztywności:

• w elementach o rozpiętości l_eff<6,0 [m] przyjmuje się:

• naprężenia w zbrojeniu (w stanie zarysowania)

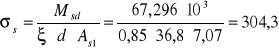
MPa

ξ=0,85 dla 0,5%<ρ>1%

• rzeczywisty stopień zbrojenia w przęśle AB:

ρ_s =

=0,96%

• dla skrajnego przęsła belki ciągłej PN-B-03264 tab.13

gdy: σ_s=250 MPa , ρ_s= 0,96% , B37

22

gdy: σ_s=304,3MPa ,


=
(uwzględniam inna wartość naprężenia)

• ze względu na sposób podparcia przyjmuje

=1,0

• Warunek kontroli ugięć:
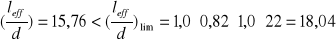
  - warunek spełniony → stan graniczny ugięć nie został przekroczony.

Przęsło BC:

W przypadku gdy: l_eff< 6,0 [m]

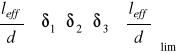
• Wskaźnik sztywności:

• w elementach o rozpiętości l_eff<6,0 [m] przyjmuje się:

• naprężenia w zbrojeniu (w stanie zarysowania)

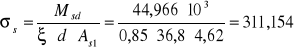
MPa

ξ=0,85 dla 0,5%<ρ>1,0%

• rzeczywisty stopień zbrojenia w przęśle BC:

ρ_s =

=0,63%

• dla wewnętrznego przęsła belki ciągłej PN-B-03264 tab.13

gdy: σ_s=250 MPa , ρ_s= 0,63% , B37

30

gdy: σ_s=160,123MPa ,


=
(uwzględniam inna wartość naprężenia)

• ze względu na sposób podparcia przyjmuję

=1,0

• Warunek kontroli ugięć:
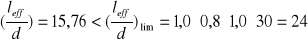
  - warunek spełniony→ stan graniczny ugięć nie został przekroczony.

Przęsło CD:

W przypadku gdy: l_eff< 6,0 [m]

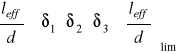
• Wskaźnik sztywności:

• w elementach o rozpiętości l_eff<6,0 [m] przyjmuje się:

• naprężenia w zbrojeniu (w stanie zarysowania)

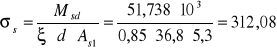
MPa

ξ=0,85 dla 0,5%<ρ>1,0%

• rzeczywisty stopień zbrojenia w przęśle CD:

ρ_s =

=0,72%

• dla wewnętrznego przęsła belki ciągłej PN-B-03264 tab.13

gdy: σ_s=250 MPa , ρ_s= 0,72% , B37

30

gdy: σ_s=189,963MPa ,


=
(uwzględniam inna wartość naprężenia)

• ze względu na sposób podparcia przyjmuje

=1,0

• Warunek kontroli ugięć:
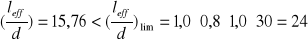
  - warunek spełniony→ stan graniczny ugięć nie został przekroczony.

Żebra zostały zaprojektowane poprawnie spełniają warunki normowe.

Oprac. Tadeusz Magiera

31

---