Równanie Bernoulliego

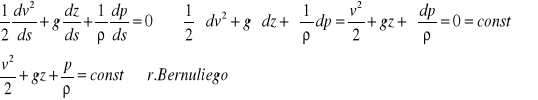
Równanie statyki płynów w stanie jednofazowym

ΔN -σ_s=0; ΔN = N ₂- N ₁; N ₁=p₁*S; N ₂=(p₁+dp)S; df=(df/ds)ds; σ_s=(dp/ds)Sds=0;

σ_s=(1/ρ)*(dp/ds)=0

Reguła Weisbacha

Liczba Reynoldsa

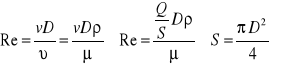
Teoria ruch płynów lepkich

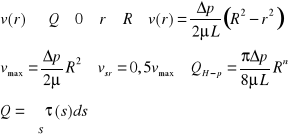
Sedymentacja

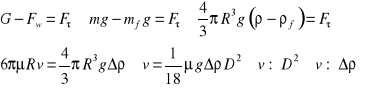
Filtracja

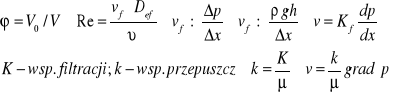
Gaz doskonały z. zachowania energii

dQ=dU+dL h=U+(pv) dh=dU+d(pv) dq=dh-v dp d(pv)=p dv+v dp

Zwężka Wenturiego

1. Temperatura - jest miarą średniej energii kinetycznej atomów lub molekuł płynu. Do pomiaru temperatury można użyć dowolnej, lecz zależnej od niej właściwo­ści płynu, jak objętość, ciśnienie, przewodność cieplna. Na przykład w termo­metrach cieczowych temperatura - jak wiadomo - jest określona przez zmianę objętości (wysokości) słupa cieczy. Podstawową jednostką temperatury bez­względnej T jest kelwin, K.

Stosowana jest również skala Celsjusza, w której pod stawową jednostką jest l °C. Obie jednostki temperatury są takie same, natomiast różnią się skale, czyli ich poziom odniesienia. Temperatura wyrażona w kelwinach jest o około 273,15 stopni większa od temperatury wyrażonej w stopniach Celsjusza.

2.Ciśnienie- jest sumarycznym efektem zderzeń molekuł z powierzchnią ściany lub ciała zanurzonego, a ściślej mówiąc, jest stosunkiem zmiany pędu molekuł zderzających się w jednostce czasu z elementem tej powierzchni do powierzchni tego elementu. Zderzenia molekuł płynu z powierzchnią są zjawiskiem złożo­nym, jednak w warunkach równowagi termodynamicznej przyjmuje się, że zmiana pędu molekuł jest normalna względem powierzchni.

W ujęciu fenomenologicznym ciśnienie p w Pa wynosi:

P=F/A gdzie: F - parcie,[N], A - powierzchnia działania parcia, [m²]

Parcie jest skierowane w stronę rozpatrywanej powierzchni. Ciśnienie jest skalarem, dopiero zaś działanie ciśnienia na konkretną powierzchnię ma charakter ukierunkowany. Podstawową jednostką ciśnienia jest paskal 1 paskal(1 Pa) =1 N/ m² =1 kg/m*s²

3. Gęstość masy (masa właściwa) ρ, czyli odwrotność objętości właściwej, jest to granica stosunku elementarnej masy płynu Δm w danym punkcie przestrzeli i elementarnej objętości ΔV zawierającej tę masę.

Hipoteza Newtona - Zgodnie z hipotezą Newtona naprężenie styczne τ jest proporcjonalne do szybkości ścinania γ 1) τ = μ*γ gdzie μ jest współczynnikiem proporcjonalności i nosi nazwę współczynnika lepkości dynamicznej. Równanie 1) przedstawia prawo tarcia Newtona.

Płyny spełniające to równanie noszą nazwę płynów newtonowskich. Z równania 1)wynika, że duże naprężenia styczne mogą wystąpić zarówno w płynach o dużej lepkości, jak i w płynach o małej lepkości, jeśli istnieją odpowiednio duże gradienty prędkości dv_x/dz. γ = dv_x/dz

Statyka

Równowaga względna cieczy- Równowagę względną cieczy w stosunku do poruszającego się naczynia rozpa­trzono na przykładzie dwóch zasadniczych ruchów naczynia, tj. ruchu postępo­wego i ruchu obrotowego. Podczas obu tych ruchów musi być spełniony waru­nek zerowej prędkości cieczy względem ścian naczynia.

Dla obu przypadków wystąpią dwie składowe jednostkowej siły maso­wej F_m. W obu rodzajach ruchów siły te są innego charakteru, lecz jedna z nich ma zawsze kierunek pionowy (przyspieszenie ziemskie), a druga poziomy. Podczas ruchu obrotowego można mówić nawet o trzech składowych, lecz z uwagi na symetrię ruchu całość sprowadza się do zagadnienia dwuwymiaro­wego.

Równanie równowagi płynu -jak już wspomniano - uwzględnia równowagę sił masowych i sił ciśnieniowych. Równanie to można wyprowadzić w różny sposób. W danym przypadku zostaną wykorzystane przytoczone w zapisy tych sił w postaci wyrażeń a)suma sił masowych działających na obszar V wynosi:
; i b)
, z których wynika: 1)
W celu przekształcenia tego równania należy skorzystać z twierdzenia Gaussa-Ostrogradskiego dla pola skalarnego, które umożliwia zamienienie całki powierzchniowej na całkę objętościową
, po podstawieniu tej wartości do wzoru 1) otrzymuje się
. Ze względu na dowolność obszaru całkowania możemy zapisać
, jest to wektorowe równanie równowagi płynu w formie różniczkowej

Kinematyka

Równanie ciągłości przepływu

Równanie ciągłości przepływu wyraża prawo zachowania masy (niezniszczalności materii). W celu wyprowadzenia tej zależności należy rozwa­żyć objętość kontrolną V, ograniczoną powierzchnią A. Dla objętości kontrolnej w przypadku ogólnym można napisać, że ogólne strumienie masy przepływającej przez powierzchnię A muszą równać się akumulacji ma Ogólny strumień masy przepływającej (dopływ minus odpływ) w różniczkowym czasie przez powierzchnię A wynosi
.

W ogólnym przypadku masa dopływająca do objętości kontrolnej nie jest równa masie opuszczającej tę objętość. Różnica między tymi wielkościami stanowi masę zaakumulowaną w objętości V. Jest ona równa
. Łącząc te dwie wielkości, otrzymuje się:
Jest to jedna z postaci równania ciągłości przepływu. Obowiązuje ono dla przepływu nieustalonego i płynu ściśliwego.

Równanie ruchu płynu doskonałego-Równanie Eulera

Podstawowe równanie ruchu płynu doskonałego wynika z zasady zachowania pędu (ilości ruchu), wg której pochodna pędu płynu zawartego wewnątrz obsza­ru V względem czasu jest równa sumie sił zewnętrznych działających na ten obszar. Zasadę tę można również wyrazić inaczej, czyli wg sformułowania d' Alemberta: siła bezwładności jest w każdej chwili równa sumie wszystkich sił zewnętrznych. Uwzględniając siły działające w płynach: a)suma sił masowych działających na obszar V wynosi:
; b)suma sił powierzchniowych działająca na całą powierzchnię A wynosi:
; c) suma sił bezwładności działających na obszar A wynosi
. Otrzymujemy:

Stosując równanie
otrzymujemy:

Ze względu na dowolność w wyborze obszaru całkowania f dla każdego elementu dV funkcja podcałkowa musi się zerować, czyli otrzymuje się:

Jest to równanie ruchu płynu doskonałego lub równanie Eulera. Określa ono zasadę (równanie) zachowania pędu. Człon po lewej stronie oznacza siły bezładności i może być przedstawiony jako pochodna substancyjna dv/dt. Pierwszy człon po prawej stronie odpowiada siłom masowym, zaś drugi człon siłom ciśnieniowym. Są to wszystko siły jednostkowe mające charakter przyspieszeń.

Dynamika

Różne formy równania Bernoulliego

Różne formy równania Bernoulliego można otrzymać po scałkowaniu równania 1)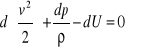
. W przypadku ruchu potencjalnego (rot v = 0) stała całkowania const jest jednakowa dla całego obszaru całkowania, natomiast w przypadku ruchu wiro­wego stała const może przyjmować różne wartości dla różnych linii prądu.

Potencjał U podczas ruchu w ziemskim polu grawitacyjnym wynika z równania U = -gz Przy czym przyjęto, że oś z jest skierowana pionowo do góry. Uwzględniając to, po scałkowaniu równania otrzymuje się 2)
Jest to równanie Bernoulliego dla płynów doskonałych. Często ta postać jest stosowana dla cieczy rzeczywistych a niekiedy również dla gazów rzeczywistych, w przypadkach gdy gęstość płynu jest w przybliżeniu stała p ≈ const.

Dla gazu ściśliwego, przyjmuje założenie o izentropowości przepływu, wobec czego korzysta się ze znanego z termodynamiki związku dp/ρ =di, gdzie di jest różniczką entalpii. Po podstawieniu tej wielkości do równania 1) i pominięciu członu d t/jako nieistotnego dla gazów otrzymuje się 3) (v²/2)+i=const=i_o Jest to równanie Bernoulliego dl. gazów ściśliwych. Symbol i_o oznacza entalpię całkowitą gazu.

Równania dla cieczy i gazów, tj. równania 2) i 3), mają formę równań zachowania energii. Odnoszą się one do jednostki masy, czyli wyrażają energię jednostki masy płynu. Po pomnożeniu członu v² /2 przez masę otrzymuje się energię kinetyczną płynu. Mnożąc człon gz w równaniu 2) przez masę, otrzymuje się energię potencjalną płynu. Suma tych członów stanowi energię mechaniczną płynu, która może ulegać zmianie kosztem wzrostu lub spadku ciśnienia. W wyniku pomnożenia członu p/ρ przez masę otrzymuje się w rezultacie iloczyn objętości rozpatrywanej masy płynu i ciśnienia. Ciśnienie nie może być traktowane jako forma energii, wobec czego człon zawierający ciśnienie przedstawia pracę sił ciśnieniowych, a zatem jest członem bilansującym zmiany energii mechanicznej płynu. Równanie Bernoulliego jest zatem równaniem zachowania energii mechanicznej podczas przepływu płynu doskonałego.

Równanie 2) pomnożone przez ρ przybiera postać

Wszystkie człony tego równania mają wymiar ciśnienia w paskalach (Pa) , oznaczają bilans energu mechanicznej i pracy sił ciśnieniowych w odniesieniu do jednostki objętości płynu. Suma tych członów nosi nazwę ciśnienia całkowitego p_o ,. Poszczególne człony tego równania mają następujące nazwy: - ciśnienie dynamiczne p_d =ρ*(v²/2); ciśnienie statyczne p, - ciśnienie hydrostatyczne p_h = g ρ z

Ciśnienie hydrostatyczne można pominąć podczas przepływu gazu oraz podczas poziomego przepływu cieczy, wówczas z równania 2) otrzymuje się ρ*(v²/2) + p = const

Równanie 2) można także odnieść do jednostki ciężaru, jeżeli po­dzieli się obie strony tego równania przez g ρ; otrzymuje się wówczas: 3) (v²/2) + (p/gρ) + z =const =h_o

Każdy z członów powyższego równania ma wymiar wysokości wobec czego człon v²/(2g) nosi nazwę wysokości prędkości; człon p/(gρ) wysokości ciśnienie; człon z - wysokości położenia. Zaś stała const - wysokości całkowitej h_o. Równanie 3) jest szczególnie użyteczne w budownictwie lądowym i wodnym, przy zagadnieniach dotyczących trans­portu wody ze zbiorników, w których od położenia zwierciadła wody zależy prędkość, a więc i strumień objętości wypływającej wody.

Zastosowanie równania Bernoulliego do pomiarów prędkości

Ważne znaczenie w przepływach mają miejsca, w których prędkość przepływu spada do zera, tj. v = 0. Są to tzw. punkty spiętrzenia, które występują z reguły przy opływie ciał stałych po stronie napływającego płynu. Położenie tych punktów przy opływach osiowosymetrycznych daje się z góry określić. Podczas zatrzymania (zahamowania) płynu w punkcie spiętrzenia następuje zamiana ciśnienia dynamicznego na ciśnienie statyczne, które zgodnie z równaniem ρ*(v²/2) + p = const , przyjmie wartość ciśnienia całkowitego p_o. Przyrząd służący do pomiaru ciśnienia całkowitego nosi nazwę sondy (rurki) Pitota.

Krytyczna liczba Reynoldsa

Jak wynika z eksperymentów, dla każdego przepływu wewnętrznego i wnętrznego, tj. przepływu w przewodzie o odpowiednim przekroju oraz opłyuu ciał o różnym kształcie, istnieje pewna wartość liczby Reynoldsa, poniżej której dany przepływ jest zawsze laminarny. Powyżej tej wartości przepływ mc utracić stateczność zależnie od poziomu zaburzeń wstępnych strumienia napływającego. Ta wartość liczby Reynoldsa nosi nazwę krytycznej liczby Reynoldsa Re_kr . W najczęściej występujących przypadkach dla przepływu w przewodach (rurach) o przekroju kołowym krytyczna liczba Reynoldsa wynosi: 1) Re_kr = v_śr*D/υ ≈ 2300 . W przewodach płaskich o wysokości (grubości) s krytyczna liczba Reynoldsa jest równa 2) Re_kr = v_śr*s/υ ≈ 1900

Przytoczone wartości Re_kr są czasem nazywane dolną wartością (Re_kr) gdyż jak wspomniano przepływ jest zawsze laminarny poniżej tej wartości. Przy daleko posuniętej ostrożności, polegającej na niedopuszczeniu do jakich­kolwiek drgań i zaburzeń przepływu, udaje się utrzymać przepływ laminarny przy znacznie większych wartościach Re, niż to podano we wzorach 1) i 2), np. podczas przepływu w przewodzie o przekroju kołowym uzyskano wartość aż Re_kr = 50000. Ta wartość jest nazywana górną wartością (Re_kr)₂. Najczęściej między (Re_kr)₁, a (Re_kr)₂ istnieje wstępna faza rozwoju ruchu turbu-lentnego. Ruch powyżej (Re_kr)₂ jest nazywany często w pełni rozwiniętym ruchem turbulentnym. Należy jednak podkreślić, że w zagadnieniach technicznych przyjmuje się, że w zakresie Re > (Re_kr)₁, istnieje zawsze przepływ turbulentny. Dla pr/ wodów o przekroju kołowym oznacza to, że przepływ turbulentny występuje dla Re > 2300.

Równanie zachowania pędu (Naviera stokesa)

Obecnie trzeba powrócić jeszcze raz do ostatniego członu równania Eulera gdyż w płynach rzeczywistych siłami powierzchniowymi są nie tylko siły ciśnienia, ale również siły związane z występowaniem naprężeń powierzchniowych.

W wyniku przekształcenia całki powierzchniowej w objętościową otrzymuje się

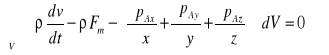
po przekształceniu otrzymujemy:

1)
ostatni człon oznacza wektor sił powierzchniowych (siły normalne i siły styczne).Równanie 1) nosi nazwę równania pędu w naprężeniach. Jest to najogólniejsze równanie zachowania pędu w formie różniczkowej dla płynu rzeczywistego.

Przepływ laminarny w przewodzie o przekroju kołowym

Zgodnie z hipotezą tarcia Newtona można zapisać
przy czym znak minus wynika stąd że wraz ze wzrostem r maleje prędkość v. Po podstawieniu i przekształceniach otrzymujemy:
, równanie to po scałkowaniu otrzymuje postać
przy czym stała całkowania może być obliczona dla warunku brzegowego, dla r=R, v=0 i stąd:
. Po podstawieniu tej wartości do wzoru na v otrzymujemy równanie rozkładu prędkości w przewodzie o przekroju kołowym
. Maksymalna prędkość występuje w osi przewodu (dla r=0) i wynosi:
.

Prędkość średnia wynosi

Strumień objętości

Opory przepływu w przewodach zamkniętych,

Podczas przepływu wewnątrz przewodu istotne znaczenie ma nie tyle znajo­mość sił stycznych, ile znajomość strat ciśnienia wywołanych działaniem tych sił. Opór przepływu w przewodach składa się z oporów tarcia i oporów miej­scowych (lokalnych). Opory tarcia występują na całej długości kanału. Podział na opory tarcia i opory miejscowe ma umowny charakter, gdyż źródłem oporów w obu przypadkach jest lepkość płynu. Całkowita strata ciśnienia pod­czas przepływu wynosi

p_str = p_strt + Σ p_strm gdzie: p_strt - strata ciśnienia wskutek tarcia; Σ p_strm - suma strat ciśnienia wskutek oporów miejscowych.

Należy obecnie wrócić do równania Bernoulliego i dostosować go do warunków przepływu rzeczywistego. Taka półempiryczna forma równa­nia Bernoulliego oddaje wielkie usługi, gdyż umożliwia zbilansowanie energii w dwóch rozpatrywanych przekrojach przewodu, jeśli znana jest energia rozproszona wskutek tarcia. W zastosowaniach praktycznych korzysta się z równania Bernoulliego, którego poszczególne wyrazy mają wymiar ciśnienia lub wysokości. Dla dwóch przekrojów 1 i 2 można zatem napisać:

Człon p_pst dotyczy strat zachodzących między przekrojem 1 a 2.

Straty ciśnienia wskutek tarcia.

Straty te nazywane są również stratami liniowymi. Są one wywołane tarciem wewnętrznym płynu w obszarze warstwy przyściennej.

Straty ciśnienia wskutek tarcia będą obliczane z wyprowadzonego w o. 5.3 wzoru Darcy-Weisbacha

1)
gdzie λ jest współczynnikiem tarcia wewnętrznego płynu (współczynnikiem oporów liniowych). Wzór ten umożliwia obliczenie strat ciśnienia wskutek tarcia p_str = p_strt w przewodzie prostoliniowym o średnicy D i długości L. Wzór Darcy-Weisbacha dotyczy zarówno przepływu laminarnego, jak i turbulentnego, przy czym w obu wypadkach obowiązują inne wartości współczynnika tarcia λ

Współczynnik tarcia wewnętrznego płynu λ. Współczynnik tarcia podczas przepływu laminarnego w przewodzie o przekroju kołowym może być wyznaczony w sposób analityczny z wzoru Hagena-Poiseuille'a . Po uwzględnieniu
wzór ten przyjmuje postać
, podstawiając liczbę Reynoldsa
otrzymujemy 2)
następnie z porównania wzorów 1) i 2) wynika że współczynnik tarcia λ podczas przepływu laminarnego wyniosi λ=64/Re

Równanie bilansu sił

---