Elektrotechnika |
Mechanika i mechatronika |
Wykłady |
Dr inż. Wojciech Homik 2011-01-01
|
Mechanika
Podział wielkość mechanicznych :
Wielkości mechaniczne dzielą się na wektory i skalary.
Skalar- jest to wielkość mechaniczna, którą możemy jednoznacznie określić poprzez podanie jej wartości liczbowej.
Wielkość ta może być przedstawiona w postaci punktu na osi współrzędnych.
Niektóre wielkości skalarne:
- temperatura
- czas
-masa
-praca
-moc
Wektor- to taka wielkość mechaniczna, którą można przedstawić za pomocą usytuowanego w przestrzeni odcinka posiadającego zwrot, kierunek, wartość i punkt przyłożenia.
W mechanice do wielkości wektorowych zaliczamy:
- prędkość
-przyśpieszenie
-siłę, moment siły itd.
Podział mechaniki
1.statyka (analiza równowagi ciał)
2. kinematyka
3. dynamika
Statyka
Podział sił w mechanice dzielimy na siły zewnętrzne i wewnętrzne.
Siły zewnętrzne dzielimy na siły:
- bierne(reakcji) i czynne
Siły wewnętrzne dzielimy na :
-siły miedzy międzycząsteczkowe
-siły napięć
Układy sił
W mechanice układy sił dzielą się na:
-układy płaskie
-układy przestrzenne
Wymienione wyżej układy dzielą się na: zbieżne, równoległe i dowolne.
Zasady statyki:
Zasada równoległoboku: dwie siły(dowolne siły) F1 i F2 przyłożone do jednego punktu można zastąpić jedną siłą wypadkową Fw, która przyłożona jest do tego samego punktu i będącą wektorem, którego miarą jest przekątna równoległoboku zbudowanego na wektorach sił składowych.
Zasada równowagi dwóch sił .
Dwie siły przyłożone do ciała sztywnego równoważą się wtedy i tylko wtedy gdy działają wzdłuż jednej prostej i mają jednakową wartość lecz przeciwne zwroty.
Zasada równoważności, działanie dowolnego układu sił przyłożonych do ciała sztywnego nie ulegnie zmianie jeżeli do tego ciała przyłożymy inny układ sił równoważących się (układ tych sił jest równy 0)
Zasada zesztywnienia, równowaga sił działających na ciało odkształcalne nie zostanie naruszona przez zmianę go na ciało sztywne
Zasada działania i przeciwdziałania każdemu działaniu towarzyszy równe co do miary ,leżące na tej samej prostej i przeciwnie skierowane przeciwdziałanie (3 zasada dynamiki)
Zasada oswobodzenia z więzów:
Każde ciało nieswobodne można umownie oswobodzić z więzów zastępując ich działanie siłami zwanymi siłami reakcji i rozpatrywać je jako ciało swobodne na które działają siły czynne i siły reakcji więzów.
Więzy i reakcje więzów
Każde ciało, które może swobodnie przemieszczać się w przestrzeni nazywamy ciałem swobodnym. Jeżeli zaś ciało nie jest w stanie swobodnie się przemieszczać ,to takie ciało nazywamy ciałem nieswobodnym.
Punkt materialny ma 3 stopnie swobody (3 współrzędne)
Odcinek ma 5 stopni swobody
Bryła(ciało sztywne) ma 6 stopni swobody
Rodzaje więzów:
Każde ciało działa na więzy ograniczające jego swobodę pewnymi siłami ,które nazywamy reakcjami więzów.
Podział więzów:
- podpory stałe, ruchome, więzy wiotkie. Wszystkie, których szczególnym przypadkiem jest pręt zamocowany przegubowo
Podpory stałe
- podparcie w skoku
- podparcie w łożysku stałym
- podparcie w przegubie kulistym
W przypadku reakcji więzów w podporach stałych znamy tylko i wyłącznie punkt, w którym ta reakcja jest zaczepiona , nie znamy kierunku zwrotu i wartości.
Podpory ruchome
- podparcie na idealnie gładkiej powierzchni
-podparcie w łożysku ruchomym
=
Łożysko
-podparcie na pryzmie
W przypadku podpór ruchomych znamy punkt zaczepienia i kierunek (normalny do stycznej w punkcie podparcia)
Więzy wiotkie
- podpory wiotkie
Ta sama wartość ,kierunek, punkt przyłożenia , zwrot
Pręt sztywny zamocowany dwustronnie przegubowo ma cechy cięgna gdyż reakcja R musi przechodzić przez oba przeguby pręta z ta różnicą, że w przeciwieństwie do cięgna pręt może być ściskany lub rozciągany . Jest zatem więzłem dwustronnym.
Rodzaje układów sił w mechanice
W mechanice układy sił dzielimy na :
*układy płaskie
*układy przestrzenne , które z kolei dzielą się na :
-układy zbieżne
- układy równoległe
- układy dowolne
Płaski zbieżny układ sił
Płaskim zbieżnym układem sił nazywamy taki układ sił, w którym kierunki działających sił przecinają się w jednym punkcie
Zbieżny układ sił składający się z dużej liczby sił można zastąpić układem prostym składającym się z mniejszej liczby sił, którego skutek działania będzie taki sam. Bywa czasami tak, że płaski zbieżny układ sił można zastąpić jedną siłą. Siłę taką nazywamy siła wypadkową. Kierunek działania tej siły przechodzi przez punkt zbieżności
Twierdzenie o sumie rzutów sił
Rzut sił na oś
Suma rzutów dowolnej liczby sił na oś, równa jest rzutom sumy tych sił na tę samą oś.
![]()
Rzut sił na oś jest równy iloczynowi tej siły przez cos kąta zawartego pomiędzy kierunkiem działania siły a osią na którą rzutowana jest siła.
![]()
kierunek działania siły ![]()
![]()
![]()
![]()
![]()
![]()
Siłę uważamy za dodatnią jeżeli jej zwrot jest zgodny ze zwrotem przyjętej osi.
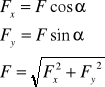
Relacja w podporach stałych
![]()
Analityczne składanie sił- twierdzenie o sumie rzutów sił
![]()
=-F1x+F2x+F4x+…+Fn-1x-Fnx
![]()
-F1y+F2y-F3y+F4y+…+Fn-1y+Fny
Warunki równowagi płaskiego zbieżnego układu sił .
Warunki te można podzielić na :
-wykreślne
-analityczne
Warunek wykreślny- wielobok sił musi być zamknięty
Warunki analityczne:
Suma rzutów wszystkich sił na oś x ma siłę równą zeru
![]()
Suma rzutów wszystkich sił na oś y ma siłę równą zeru
![]()
Twierdzenie o 3 siłach :
Trzy siły znajdują się w równowadze statycznej wtedy i tylko wtedy jeżeli działają na jednej płaszczyźnie a ich kierunki działania przecinają się w jednym punkcie i tworzą wielobok sił zamkniętych.
Przykład
![]()
![]()
Q=10[N]
S1=?
S2=?
![]()
σr =![]()
≤ kr σr = ![]()
≤ kr F[N] A[m2] kr[MPa]
![]()
![]()
≤ kr
d ≥ 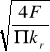
![]()
![]()
![]()
F1-F2=0 => F1=F2
Dla symetrycznego układu sił:
S1=S2 ,S3=S6, S4=S5, S1'=S2'
Warunki równowagi równoległego układu sił
Równoległym układem sił nazywamy taki układ sił w którym kierunki działających sił są do siebie równoległe.
Warunki równowagi równoległego układu sił są szczególnego przypadku układu dowolnego. Taki równoległy układ sił możemy zastąpić jedną siłą
: siłą wypadkową Fw którą należy przyłożyć w miejscu przecięcia się kierunków
działających sił, by jej działanie było równoważne układowi który zastępuje.
Wielobok sznurowy
Układ równoległy = Układ dowolny
Pojęcie siły bezwzględnej względem dowolnie wybranego bieguna.
r - najmniejsza odległość między wektorem ![]()
a środkiem O
![]()
Moment siły F względem bieguna nazywamy iloczyn wartości tej siły przez odległość(najmniejsza odległość) jaka dzieli kierunek działającej siły od przyjętego bieguna.
Własności momentu:
Moment sił jest równy iloczynowi sił przez ramie, jest to wielkość wektorowa.
Kierunek momentu sił jest prostopadły do płaszczyzny utworzonej przez kierunek siły i biegun.
Moment siły nie ulega zmianie gdy się przesuwamy w wzdłuż jej kierunku działania,
Moment sił względem dowolnego punktu leżącego na kierunku działania siły jest równy zero.
Prawa sił i jej własności:
Parą sił nazywamy układ dwóch sił, których kierunki działania są do siebie równoległe, wartości sił są jednakowe lecz mają przeciwne zwroty,
![]()
Moment par sił jest równy iloczynowi jednej z sił prze odległość jaką dzieli kierunki pary sił. Pary sił nie można zastąpić ani zrównać siłą wypadkową. Każdą parę sił można zastąpić momentem i odwrotnie.
Każdy moment można zastąpić pasą sił. Skutek działania pary sił nie zmienia się jeżeli daną pare przeniesiemy w dowolne inne miejsce w jej płaszczyźnie.
Płaszczyznę w przestrzeni jednoznacznie można określić przez:
Trzy punkty.
Prostą i punkt.
Dwóch prostych (dowolnych)
Wektor momentu pary sił jest prostopadły do płaszczyzny określonej kierunkami pary sił
Warunki równoległego układu sił.
Warunki wykreślne:
wielobok sił musi być wielobokiem zamkniętym.
wielobok sznurowy musi być zamknięty.
Warunki analityczne:
suma rzutów wszystkich sił na oś X ma się równać zero.
suma rzutów wszystkich sił na oś Y ma się równać zero.
suma momentów wszystkich sił względem dowolnie wybranego bieguna ma się równać zero.
Warunki wykreślne:
wielobok sił zamkniętych .
wielobok sznurowy zamknięty.
Warunki analityczne:
algebraiczna suma wszystkich sil na os x ma sie równać 0wielobok sznurowy zamknięty.
algebraiczna suma wszystkich sil na os y ma sie równać 0wielobok sznurowy zamknięty.
suma momentów wszystkich sil wzg. dowolnie wybranego bieguna ma sie równać 0.
Wały maszynowe
Wały napędowe
Sprężyny
Śruby
Klucze do zamków
Zapis matematyczny:
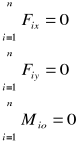
Przykład:
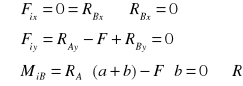
Płaski dowolny układ sił jest szczególnym przypadkiem dowolnego układu sił w którym kierunki działających sił są do siebie równoległe. W przypadku dowolnego układu sił kierunki działających sił nie są do siebie równoległe. Dowolny układ sił stanowi kombinacje płaskiego zbieżnego i płaskiego równoległo układu sił.
Wobec powyższego nasuwa się wniosek, że w dowolnym układzie sił niektóre kierunki działających sił mogą się ze sobą przecinać ,ale też mogą być ze sobą równoległe. By dowolny układ sił był w równowadze muszą być spełnione następujące warunki.
![]()
![]()
![]()
jak dla równoległego układ sił
Przykład:
Wyznaczyć wartości reakcji w punktach A i B dla konstrukcji obciążonej jak na rys.
![]()
![]()
![]()
Sprawdzenie
Podstawić wyznaczone wartości do powyższych równań.
Przestrzenny układ sił przez analogie do płaskich układów sił można podzielić na zbieżne układy sił, równoległe układy sił i układy dowolne.
Zbieżny przestrzenny układ sił
Rzutowanie sił na trzy osie prostokątnego układu współrzędnych :
Fx = Fcosα
Fy = Fcosβ
Fz = Fcosγ
Wszystkie trzy równania podnieśmy do kwadratu i dodajmy stronami.
![]()
![]()
=![]()
![]()
Z trygonometrii wynika, że suma kwadratów cosinusów kierunkowych kątów, jakie dowolna prosta tworzy z osiami xyz jest równa jedności czyli możemy zapisać:
![]()
![]()
![]()
![]()
Cosinusy kierunkowe
![]()
![]()
![]()
Niech będzie dany przestrzenny układ sił których kierunki działania przecinają się w jednym punkcie.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Twierdzenie:
Rzut geometryczny sumy S pewnej liczby sił na dowolną oś jest równoważny sumie rzutów wszystkich sił składowych na tę oś.
W myśl powyższego Twierdzenia możemy napisać:
![]()
![]()
![]()
Uwzględniając rozważania przeprowadzone dla jednej siły znajdującej się w układzie trzech rzutów i trzech osi prostokątnych możemy napisać, że
![]()
Zaś kosinusy kierunkowe są równe:
cosα=![]()
cosβ=![]()
cosγ=![]()
Wypadkowa ![]()
podanych 3 sił zbieżnych będzie miała te samą wartość, ten sam kierunek oraz zwrot co suma ![]()
. Można zatem powiedzieć, że wyznaczona suma ![]()
, przeniesiona do punktu zbieżności jest siłą wypadkową tego układu sił zbieżnych, w szczególnych wypadkach wypadkową siłą ![]()
przestrzennego zbieżnego układu sił może się równać zero. W takim przypadku analizowany (rozpatrywany) układ sił będzie w równowadze:
![]()
= ![]()
W szczególnych przypadkach:
![]()
Zależność ta będzie spełniona wtedy i tylko wtedy kiedy
![]()
![]()
![]()
W innym przypadku nie biorąc powyższe pod uwagę można sformułować następujące warunki równowagi dla przestrzennego zbieżnego układu sił.
![]()
![]()
![]()
![]()
Oznaczenie:
Siła skupiona F
F
Układ ten jest to zbiór sił równoległych.
Wypadkowa siła Q dla prostokątnego układu zaczepiona jest w punkcie Z. Jest równa co do wartości iloczynowi :
![]()
wydatku q i długości l której ten wydatek jest rozłożony.
Przykład dla płaskiego zbieżnego układu sił.
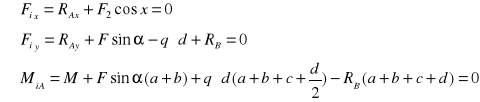
Przykład
Wyznaczyć wartości w elementach konstrukcji obciążoną siłą skupioną.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Twierdzenie momentu sił względem osi
Momentem siły względem osi nazywamy iloczyn rzutu tej siły na płaszczyznę prostopadłą do osi przez odległość tego rzutu od osi
Moment siły względem osi jest równy zero gdy :
- siła F jest równoległa do osi l ![]()
- kierunek działania siły przecina się z osia l r=0
Moment siły względem osi jest równy zero wtedy, gdy siła i oś leżą w jednej płaszczyźnie.
Redukcja dowolnego układu sił do siły i pary sił:
Do punktu A ciała sztywnego przykładamy siły P. Do dowolnego punktu 0 przyłożymy dwie równe co do wartości, lecz przeciwnie skierowane siły P i -P. Otrzymujemy wówczas układ sił składających się z siły P przyłożonej do początku układu współrzędnych 0 oraz pary sił Pi- P przyłożonych do punktu A i 0. Moment powyższej pary sił jest równy momentowi względem początku układu współrzędnych O danej siły P przyłożonej do punktu A czyli :
![]()
Twierdzenie
Wobec powyższego możemy powiedzieć, że każdą siłę działającą na ciało sztywne możemy sprowadzić do dowolnie wybranego punktu 0 przykładając parę sił o momencie równym momentowi siły względem punktu 0
W przypadku gdy do ciała sztywnego przyłożone są w punktach A1,A2,…An siły P1, P2,… Pn dowolnie skierowane w przestrzeni możemy postępując analogicznie jak wyżej, wszystkie te siły sprowadzić do środka redukcji 0.
W wyniku otrzymujemy układ sił zbieżnych P1, P2,…Pn
Przyłożonych do punktu 0, oraz n par sił o momentach równych Mo, Mo2, Mo3,… Mon , przy czym Mio oznacza tu 0 zwana siłą wypadkową. Podobnie układ par sił równoważny jest jednej parze o momencie Mo, równym sumie geometrycznej momentów tych par.
Mamy więc:
R=P1+P2+…+Pn=![]()
Mo=Mo1+Mo2+…+Mno=r1 x P1+r2 x P2+…+rn x Pn= ![]()
Twierdzenie
Dowolny układ sił działających na ciało sztywne możemy zastąpić R przyłożoną do dowolnie wybranego środka redukcji 0, równą sumie geometrycznej i wszystkich sił układu, oraz parą sił o momencie Mo i równym sumie geometrycznej momentów tych sił względem środka 0
Siłę R nazywamy wektorem głównym, zaś moment Mo momentem głównym względem środka 0
W przypadku gdy znane są składowe sił w układzie współrzędnych (prostokątnym), składowe wektora P wyznaczamy z zależności :
![]()
![]()
![]()
![]()
cosinusy kierunkowe :
![]()
![]()
![]()
![]()
- kąty, które tworzy wektor R z osiami.
Podobnie można wyznaczyć wektor momentu głównego
![]()
![]()
![]()
![]()
Cosinusy kierunkowe
![]()
![]()
![]()
Warunki równowagi dowolnego przestrzennego układu sił:
W ogólnym przypadku sił działających na ciało sztywne równowaga możliwa jest tylko wtedy, gdy suma geometryczna tych sił jest równa zeru oraz gdy suma geometryczna ich momentów względem dowolnego punktu o jest równa zero.
Przyjmując jako punkt o początek układu współrzędnych otrzymujemy:
![]()
![]()
![]()
![]()
![]()
![]()
Przykłady:
Zredukować układ sił do wektora i momentu głównego oraz wyznaczyć kosinusy kierunkowe wyznaczonych wektorów.
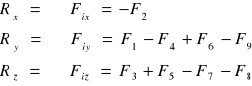
![]()
![]()
![]()
![]()
Momenty względem osi x:
![]()
Momenty względem osi y:
![]()
Momenty względem osi z:
![]()
![]()
![]()
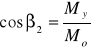
![]()
Punkt materialny - to ciało które przy badaniu jego ruchu potraktowano jako ciało o wymiarach tak małych, że można je uważać za punkt w sensie geometrycznym, mające jednak własności mechaniczne (masa).
Ciało sztywne - to ciało które nie odkształca się a więc pod działaniem dowolnie dużych sił, odległości wzajemne elementów tego ciała pozostają stale niezależne od działających sił.
Zasady dynamiki Newtona
Punkt materialny na który nie działają siły, lub działają siły równoważące się pozostaje w spoczynku lub porusza się ruchem jednostajnym po linii prostej.
Przyspieszenie punktu materialnego ma wartość proporcjonalną do wartości siły działającej na ten punkt ma kierunek tej siły
F = m p
Siły, które wywierają na siebie dwa punkty materialne są równe co do wartości, są skierowane wzdłuż prostej łączącej te dwa punkty oraz zwrócone przeciwnie (akcja i reakcja).
Prawa zaprezentowane powyżej zostały sformułowane przez Newtona w 1687r i zaprezentowane w pracy pt ''Matematyczne zasady filozofii naturalnej''
Kinematyka: jest opisem ruchu bez wnikania w związki między ruchem i siłami
Dynamika: bada związki między siłami a ruchem, korzystając z pojęć kinematycznych
Jeżeli do 2 punktów przyłożymy siłę(taka samą) to w myśl drugiej zasady dynamiki Newtona możemy zapisać
![]()
, ![]()
p1m1=F , p2m2=F
p1m1= p2m2
![]()
zatem:
przyspieszenie udzielone 2 pkt. materialnym pod działaniem tej samej siły jest odwrotnie proporcjonalne do mas tych pkt. Masę określoną na podstawie drugiej zasady dynamiki i mierzoną przez porównanie przyspieszeń nazywamy masą bezwzględną
![]()
Analityczny opis ruchu punktu swobodnego
ruch punktu będzie określony, jeżeli współrzędne tego punktu będą określone dla każdej chwili z badanego przedziału czasu
x = x(t) y = y(t) z = z(t)
Pomiędzy opisem wektorowym i analitycznym istnieje odpowiedniość
współrzędne pkt. obserwowanego x, y, z są w tym układzie rzutami wektora wodzącego na osie
![]()
Prędkość punktu- prędkość punktu jest pochodną wektora wodzącego względem czasu
![]()
V = ![]()
+![]()
+ ![]()
Składowe wektora prędkości
![]()
=![]()
![]()
=![]()
Przyspieszenie
![]()
=![]()
![]()
=![]()
![]()
=![]()
Prędkość
![]()
=![]()
x=![]()
y=![]()
Przemieszczenie
z=![]()
Stałe całkowania C1 do C6 wyznaczamy z warunków początkowych.
Ruch pod działaniem siły zależnej od czasu F =F(t)
![]()
=![]()
![]()
=![]()
![]()
=![]()
Równania te mają jednakową postać zatem dla przykładu w celu wyznaczenia prędkości i drogi rozwiązujemy przykładowo jedno z nich.
![]()
=![]()
![]()
=![]()
x=![]()
Ruch pod działaniem siły zależnej od położenia punktu
F=F(t)
Fx=Fx (x,y,z)
Fy=Fy (x,y,z)
Fz=Fz (x,y,z)
Przy tego typu zależności rozwiązania ruchu znane są tylko w przypadkach szczególnych
Równanie ruchu punktu materialnego nieswobodnego
Ciało na które zostały nałożone pewne ograniczenia nazywamy ciałem nieswobodnym. Uwzględniając zatem to w II zasady dynamiki Newtona możemy napisać:
Mp=F+R
m![]()
=Fx + Rx
m![]()
=Fy + Ry
m![]()
=Fz + Rz
Równanie ruchu nieswobodnego układu punktów materialnych II zasada dynamiki Newtona
mi pi = Fi + Wi
mi pix = Fix + Wix
mi piy = Fiy + Wiy
mi piz = Fiz + Wiz
Równanie ruchu nieswobodnego układu materialnego
mi pi = Fi + Wi + Ri
mi pix = Fix + Wix + Rix
mi piy = Fiy + Wiy + Riy
mi piz = Fiz + Wiz + Riz
Prawo zmienności pędu punktu materialnego
mp=F
P=![]()
m![]()
=F
![]()
(mV) = F
mV = B [kg ![]()
]
![]()
(B) = F
![]()
= F
Pochodna pędu punktu materialnego względem czasu jest równa sile działającej na ten punkt
![]()
x = ![]()
(mVx) = Fx = ![]()
(![]()
x)
![]()
y = ![]()
(mVy) = Fy = ![]()
(![]()
y)
![]()
z = ![]()
(mVz) = Fz = ![]()
(![]()
z)
![]()
dB=Fdt Fdt - element wektora impulsu siły
dB=di
Przyrost pędu punktu materialnego jest równy elementarnemu impulsowi siły działającej na ten punkt
Pojęcie krętu-prawo zmienności krętu
Moment wektora punktu materialnego względem punktu 0 nazywamy krętem punktu materialnego względem tego punktu.
K = M0(B) = r × mV [(m2*kg)/s]
Praca
Praca elementarna
d'l = FdV
d'l = F![]()
V![]()
dt jest to iloczyn skalarny
Vdt = dr
d'l = Fxdx+Fydy+Fzdz
d'l = (FxVx+FyVy+FzVz)dt
Moc
Mocą siły nazywamy stosunek elementarnej pracy wykonanej przez tę siłę ,do czasu w którym ta praca została wykonana.
![]()
Sprawność
![]()
Energia kinetyczna
Ek=1/2 mV2
Mp = F /![]()
dr
mp![]()
dr=Fdr
mp![]()
dr=d'l
m![]()
dv/dt![]()
dr = mdv![]()
dr/dt = mVdV
dEk = d'l
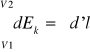
mV2/2 -mV12/2 =LAB
EkA - EkB = LAB
Przyrost energii kinetycznej poruszającego się punktu równy jest pracy siły działającej na ten punkt na drodze jaką ten punkt przebył.
Rozciąganie i ściskanie
Rozważmy zagadnienia rozciągania i ściskania na przykładzie prętów o przekroju kwadratowym.
Odkształcenia wzdłużne
Przyjmujemy, że przed obciążeniem długości prętów wynosiły , zaś po przyłożeniu obciążenia wymiary prętów uległy zmianie L1, h1
Różnicą długości końcowej i początkowej nazywamy wydłużeniem całkowitym
ΔL=L1-L
Przy rozciąganiu Δ „+”
Przy ściskaniu Δ „-”
Dzieląc wzdłużnie (skrócenie) całkowite ΔL przez długość początkową L otrzymujemy wydłużenie (skrócenie) względne lub jednostkowe ε
![]()
Wydłużenie jednostkowe jest liczbą bezwymiarową niejednokrotnie podawaną w %
![]()
Odkształcenie poprzeczne
Podczas rozciągania oprócz zmiany długości zmianie ulega również h do h1. Różnica pomiędzy grubością końcową h1 a początkową h nazywa się zwężeniem całkowitym ![]()
![]()
Stosunek zwężenia całkowitego do grubości początkowej nazywamy zwężeniem jednostkowym ![]()
Przy rozciąganiu ε1=”-„
Przy ściskaniu ε1=”+„
Stosunek wydłużenia jednostkowego do zwężenia jednostkowego nazywamy współczynnikiem odkształcenia poprzecznego lub liczba Poissona ![]()
![]()
Naprężenia na przekrojach prostopadłych do osi. Prawo Hooke'a
W dowolnym przekroju rozciąganym lub ściskanym prostopadłym do osi siły wewnętrzne maja wypadkową R normalną (prostopadłą) do tego przekroju
W przekrojach prostopadłych do osi rozciągania występują tylko naprężenia normalne
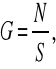
N= F S- pole przekroju poprzecznego
Zależności pomiędzy naprężeniem przy rozciąganiu (ściskaniu G, a odkształceniem f została opisana prawem Hooke'a, które brzmi:
Wydłużenie ![]()
jest wprost proporcjonalne do działającej siły F oraz długości elementu l, zaś odwrotnie proporcjonalne do pola przekroju poprzecznego tego elementu.
![]()
E-moduł sprężystości wzdłużnej (model Younga)
Należy pamiętać, że podczas rozciągania pole przekroju elementu rozciąganego zmniejsza się, zatem naprężenia rzeczywiste w elemencie, odniesione do przekroju rzeczywistego będzie większe od naprężenia odniesionego do przekroju początkowego
![]()
Fakt ten można pominąć w obszarze odkształceń sprężystych
Kąt β = nachylenie wykresu naprężeń do osi odkształcenia jednostkowego ε charakteryzuje moduł sprężystości wzdłużnej
![]()
![]()
![]()
![]()
![]()
Naprężenia dopuszczalne :
Granica proporcjonalności Hooke'a
![]()
[MPa] naprężenie
Granica plastyczności Re
![]()
Wytrzymałość na rozciąganie Rm
![]()
Dopuszczalne naprężenia obliczamy z zależności :
![]()
x-współrzędne bezpieczeństwa
Przy rozciąganiu
Materiały kruche ![]()
Materiały plastyczne ![]()
Środki ciężkości
Środek ciężkości sił równoległych
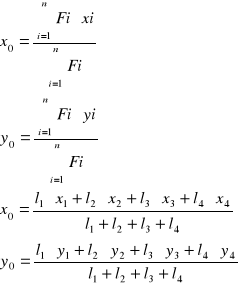
Środek ciężkości figury płaskiej
Liczymy z całki![]()
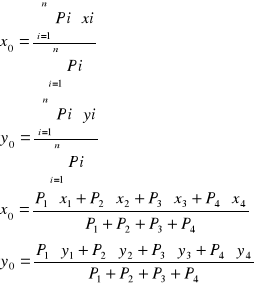
Środek ciężkości linii łączących
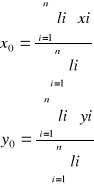
Zginanie belek płaskich
Moment siły powoduje zgięcie belki
Przykład 1:
Wyznaczyć wartości momentów gnących i sił tnących(sporządzić wykres obliczonych wartości)
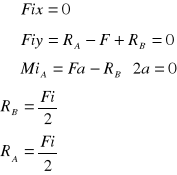
Obliczanie momentów gnących
1
![]()
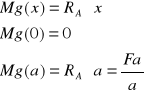
2
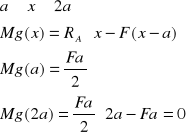
Siły tnące
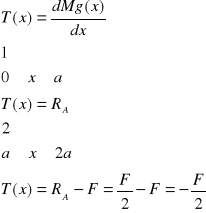
Przykład 2:
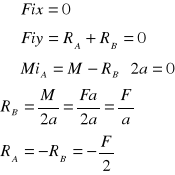
Obliczanie momentów gnących
1
![]()
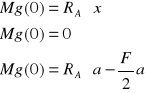
2
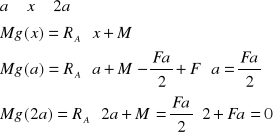
Siły tnące
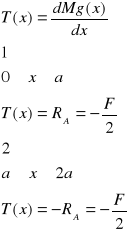
Przykład 3:
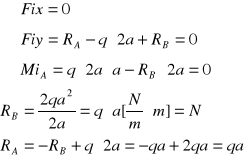
Obliczanie momentów gnących
1
![]()
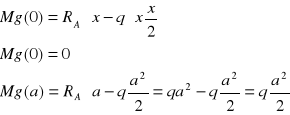
2
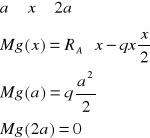
Siły tnące
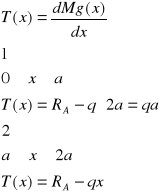
Przykład 4:
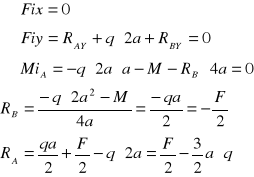
Wykład skręcanie :
Ze skręcaniem spotykamy się praktycznie na każdym kroku. Skręcaniu a dokładnie działanie momentowi skręcającemu podlegają:
Rozpatrzmy pręt, który jednym końcem utwierdzimy, zaś na drugim końcu przyłożona para sił w pł. przekroju poprzecznego pręta. Ramię pary sił oznaczmy przez „a”.
Równowaga tej części wałka nastąpi tylko wtedy (wał nie ulegnie zniszczeniu) gdy na drugim końcu wału będzie moment równy co do wartości działającemu, lecz przeciwnie skierowany. Moment taki nazywamy momentem skręcającym i oznaczamy Ms.
Jak wiemy parę sił możemy zastąpić momentem, którego działanie będzie takie samo jak pary sił zatem możemy powyższy rysunek zastąpić rysunkiem postaci
Wartość momentu Ms w każdym przekroju rozpatrywanego wałka jest jednakowa i wynosi
M0=M=Fa
Co możemy przedstawić na wykresie w kształcie prostokąta, którego rzędne w przyjętej podziałce przedstawiają momenty skręcające w poszczególnych przekrojach pręta. Wykres taki nazywamy wykresem momentów skręcających.
Naprężenia w przekrojach pręta skręcanego
Rozpatrzmy analogiczny pręt jak poprzednio na którego tym razem na powierzchni naniesione zostaną tworzące i prostopadłe do nich okręgi (pokryjemy pręt siatką z prostokątów).
Naprężenia w przekrojach pręta skręcającego
Rozpatrzmy analogiczny pręt jak poprzednio na powierzchnię którego naniesione zostaną tworzące i prostopadłe do nich okręgi(pokryjemy pręt siatką prostokątów)
Przy przyłożeniu na swobodny koniec pręta momentu Ms (pary sił w płaszczyźnie przekroju) pręt się odkształca. Przy małych odkształceniach promienie nie zmieniają swoich średnic, obracają się jedynie względem siebie. W takim przypadku wszystkie tworzące walca przechodzą w tzw. Linie śrubową. Również w takim przypadku odległość pomiędzy poszczególnymi okręgami nie ulega zmianie.
Ten obrót poszczególnych krążków (okręgów) względem siebie jest spowodowany występowaniem naprężeń stycznych. O istnieniu takich naprężeń informuje nas również fakt występowania odkształcenia postaciowego poszczególnych prostokątów prostokątnej siatki naniesionej na skręcany pręt. Pierwotny element warstwy powierzchniowej ABCD zmienia się w skrośnokątny A'B'C'D'
Największe naprężenia styczne
Naprężenia styczne w prętach skręcanych w poszczególnych punktach przekroju nie są jednakowe. W środku przekroju poprzecznego są one równe zeru, gdyż oś pręta się nie odkształca. Im dalej od osi tym naprężenia są większe.
Naprężenia styczne zmieniają się proporcjonalnie do odległości od środka przekroju.
Na elementarnym polu oddalonym od środka pręta o t (np.=1) naprężenie styczne jest równe To, zaś na elementarnym polu ![]()
oddalonym od środka pręta skręcanego o gi ![]()
I proporcji możemy zatem zapisać :![]()
T=1 => ![]()
Moment skręcający jest równy sumie momentów wszystkich sił działających w płaszczyźnie przekroju względem środka tego przekroju:
![]()
Gdzie
![]()
-siła styczna działająca na elementarnym polu
![]()
![]()
![]()
biegunowy moment bezwładności względem środka przekroju
![]()
Ms=![]()
I0
![]()
W odległości g od środka naprężenie styczne jest równe
![]()
Zatem możemy napisać :
![]()
Maksymalne naprężenie styczne występuje gdy g= r zatem możemy napisać:
![]()
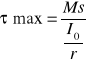
Stosunek biegunowego momentu bezwładności do
![]()
= ![]()
przekroju kołowego nazywamy wytrzymałości przekroju na rozciąganie
![]()
![]()
Odkształcenia pręta skręcanego
Rozważmy promień pręta, który został utwierdzony i obciążony momentem Ms
Dla małych odkształceń możemy zapisać, że :
![]()
![]()
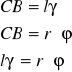
Zgodnie z prawem Hooke'a mamy
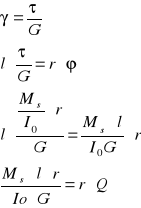
Całkowity kąt skręcania wału wyraża się w radianach i jest równy
![]()
Całkowity kąt skręcania wału jest proporcjonalny do momentu skręcającego i długości wałka, a odwrotnie proporcjonalny do sprężystości postaciowej G i biegunowego momentu bezwładności przekroju.
Iloczyn G![]()
I0 -nazywamy sztywnością skrętna . W zależności od rozwiązania konstrukcyjnego dopuszczalne kąty skręcania g wynoszą od 0,2° do 2° na długości 1 [m]
Obliczanie wartości skręcanych :
![]()
- warunek wytrzymałości wału na skręcanie
Warunek sztywności wału skręcanego
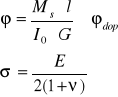
str. 37
str. 52
str. 47
β
x4
x3
x2
x1
y4
y3
F4
F1
F3
F2
y1
y2
x
y
x
y2
y1
y3
x1
x2
x3
y
y
x
y2
y1
y3
x2
x3
y4
x4
x1
x
Moment gnący dodatni
Moment gnący ujemny
Siły gnące dodatnie
Siły gnące ujemne
-Fa/2
Fa/2
RB
B
A
RA
A
RA
A
Fa/2
Mg(x)
F
a
RA
a
a
F
x
y
4
3
2
1
-Fa/2
RB
B
A
RA
A
RA
A
-Fa/2
x
x
Fa/2
M
a
RA
a
a
M
x
y
4
3
2
1
B
A
A
q
q
q
qa
-qa
x
x
Mg(x)
a
RA
RA
a
a
RB
RA
x
y
4
3
2
1
M
M
B
A
A
q
q
q
x
x
a
RA
RA
2a
2a
RB
RA
x
y
2
1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Toksykologia - Wykład 3 - Mechanizmy działania, szkoła bhp, Toksykologia
m010p, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m014a, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m002b, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
TEMATY WYKŁADÓW, Mechanika
MachBarwi2, Politechnika, Sprawozdania, projekty, wyklady, Mechanika Ogolna
ZASADA ZACHOWANIA PĘDU, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
Biochemia wykład 8 Mechanizmy adaptacyjne mikroorganizmów
WYKŁAD Mechanika Ogólna Część IV
WYKŁAD Mechanika Ogólna Część VII
WYKŁAD Mechanika Ogólna Część III
WYKŁAD Mechanika Ogólna Część II
Errata skrypt Wyklady z mechaniki ogolnej
więcej podobnych podstron